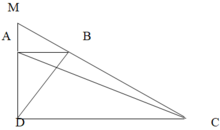
Chìnhinh thang ABCD, đáy AB = 1/3 DC. Kéo dài DA và CB cắt nhau tại O. Diện tích AOB là 5 cm2 . Tinh diện tích hình thang ABCD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 5 2018
\(\frac{ }{\frac{ }{ }\frac{ }{ }\frac{ }{ }}\)Thằng LHM xàm thế âm điểm là phải rồi ^.^
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
23 tháng 5 2022
Hai tg ABC và tg ACD có đường cao từ C->AB = đường cao từ A->CD nên
\(\dfrac{S_{ABC}}{S_{ACD}}=\dfrac{AB}{CD}=\dfrac{1}{3}\Rightarrow S_{ACD}=3xS_{ABC}\)
\(\Rightarrow S_{ABCD}=S_{ABC}+S_{ACD}=S_{ABC}+3xS_{ABC}=4xS_{ABC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{4}xS_{ABCD}\)
Kéo dài AB, từ C dựng đường thẳng song song với AD cắt AB kéo dài tại E => AECD là hình chữ nhật
\(\Rightarrow AE=CD\Rightarrow AB=\dfrac{1}{3}CD=\dfrac{1}{3}AE\Rightarrow AB=\dfrac{1}{2}xBE\)
Hai tg ABC và tg EBC có chung đường cao từ C->AB nên
\(\dfrac{S_{ABC}}{S_{EBC}}=\dfrac{AB}{BE}=\dfrac{1}{2}\)
Hai tg này có chung BC nên
\(\dfrac{S_{ABC}}{S_{EBC}}=\) đường cao từ A->BC = đường cao từ E->BC\(=\dfrac{1}{2}\)
Hai tg AMC và tg EMC có chung MC nên
\(\dfrac{S_{AMC}}{S_{EMC}}=\)đường cao từ A->BC = đường cao từ E->BC\(=\dfrac{1}{2}\)
Hai tg AMC và tg AME có chung AM và đường cao từ C->AD = đường cao từ E->AD nên
\(S_{AMC}=S_{AME}\Rightarrow\dfrac{S_{AME}}{S_{EMC}}=\dfrac{1}{2}\)
Hai tg AME và tg EMC có đường cao từ C->AD = đường cao từ M->EC nên
\(\dfrac{S_{AME}}{S_{EMC}}=\dfrac{AM}{EC}=\dfrac{1}{2}\)
Hai tg MAB và tg ABC có chung AB nên
\(\dfrac{S_{MAB}}{S_{ABC}}=\) đường cao từ A->AB / đường cao từ C->AB = \(\dfrac{AM}{EC}=\dfrac{1}{2}\)
\(\Rightarrow S_{MAB}=\dfrac{1}{2}xS_{ABC}=\dfrac{1}{2}x\dfrac{1}{4}xS_{ABCD}=\dfrac{1}{8}xS_{ABCD}=2,5cm^2\)