Chứng tỏ với x ≠ 0 và x ≠ ± a (a là một số nguyên), giá trị của biểu thức: P = a − x 2 + a 2 x + a . 4 a x − 8 a x − a là một số chẵn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Rút gọn biểu thức ta có :
\(\left(a-\frac{x^2+a^2}{x+a}\right).\left(\frac{2a}{x}-\frac{4a}{x-a}\right)\)
\(=\frac{a\left(x+a\right)-\left(x^2+a^2\right)}{x+}.\frac{2a\left(x-a\right)-4a.x}{x\left(x-a\right)}\)
\(=\frac{ax+a^2-x^2-a^2}{x+a}.\frac{2ax-2a^2-4ax}{x\left(x-a\right)}\)
\(=\frac{ax-x^2}{x+a}.\frac{-2a^2-2ax}{x\left(x-a\right)}\)
\(=\frac{-\left(x^2-ax\right)}{\left(x+a\right)}.\frac{-\left(2a^2+2ax\right)}{x\left(x-a\right)}\)
\(=\frac{\left(x^2-ax\right).\left(2a^2+2ax\right)}{x\left(x+a\right)\left(x-a\right)}\)
\(=\frac{x\left(x-a\right).2a\left(a+x\right)}{x\left(x+a\right)\left(x-a\right)}\)
\(=2a\)
Với a là một số nguyên thì giá trị biểu thức bằng 2a là một số chẵn.
Chúc bạn học tốt !!!

Rút gọn biểu thức ta có:
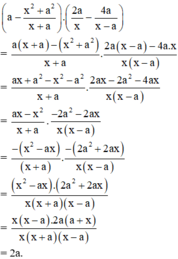
Với a là một số nguyên thì giá trị biểu thức bằng 2a là một số chẵn.

a: Thay x=2/3 vào A, ta được:
\(A=\dfrac{3\cdot\dfrac{2}{3}+2}{\dfrac{2}{3}}=\dfrac{2+2}{\dfrac{2}{3}}=4\cdot\dfrac{3}{2}=6\)
b: \(B=\dfrac{x^2+1}{x^2-x}-\dfrac{2}{x-1}\)
\(=\dfrac{x^2+1}{x\left(x-1\right)}-\dfrac{2}{x-1}\)
\(=\dfrac{x^2+1-2x}{x\left(x-1\right)}\)
\(=\dfrac{\left(x-1\right)^2}{x\left(x-1\right)}=\dfrac{x-1}{x}\)
c: P=A:B
\(=\dfrac{3x+2}{x}:\dfrac{x-1}{x}=\dfrac{3x+2}{x}\cdot\dfrac{x}{x-1}=\dfrac{3x+2}{x-1}\)
Để P là số nguyên thì \(3x+2⋮x-1\)
=>\(3x-3+5⋮x-1\)
=>\(5⋮x-1\)
=>\(x-1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{2;0;6;-4\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{2;6;-4\right\}\)
Thay x=2 vào P, ta được:
\(P=\dfrac{3\cdot2+2}{2-1}=\dfrac{8}{1}=8\)
Thay x=6 vào P, ta được:
\(P=\dfrac{3\cdot6+2}{6-1}=\dfrac{18+2}{5}=\dfrac{20}{5}=4\)
Thay x=-4 vào P, ta được:
\(P=\dfrac{3\cdot\left(-4\right)+2}{-4-1}=\dfrac{-12+2}{-5}=\dfrac{-10}{-5}=2\)
Vì 2<4<8
nên khi x=-4 thì P có giá trị nguyên nhỏ nhất

1: Thay x=16 vào A, ta được:
\(A=\dfrac{6-2\cdot4}{4-5}=\dfrac{-2}{-1}=2\)

\(C=\frac{2\left(x-1\right)^2+1}{\left(x-1\right)^2+2}\)
a, Ta thấy \(\left(x-1\right)^2\ge0\forall x\Rightarrow\hept{\begin{cases}2\left(x-1\right)^2+1\ge1>0\\\left(x-1\right)^2+2\ge2>0\end{cases}}\)
\(\Rightarrow C>0\forall x\)(đpcm)
b, \(C=\frac{2\left(x-1\right)^2+1}{\left(x-1\right)^2+2}=\frac{2\left(x-1\right)^2+4-3}{\left(x-1\right)^2+2}=2-\frac{3}{\left(x-1\right)^2+2}\)
\(C\in Z\Leftrightarrow2-\frac{3}{\left(x-1\right)^2+2}\in Z\)
\(\Leftrightarrow\frac{3}{\left(x-1\right)^2+2}\in Z\)Lại do \(\left(x-1\right)^2+2\ge2\)
\(\Leftrightarrow\left(x-1\right)^2+2\inƯ\left(3\right)=\left\{3\right\}\)
\(\Leftrightarrow\left(x-1\right)^2\in\left\{1\right\}\)
\(\Leftrightarrow x\in\left\{0\right\}\)
....
c, \(C=2-\frac{3}{\left(x-1\right)^2+2}\)
Ta có : \(\left(x-1\right)^2+2\ge2\Rightarrow\frac{3}{\left(x-1\right)^2+2}\le\frac{3}{2}\)
\(\Rightarrow C=2-\frac{3}{\left(x-1\right)^2+2}\ge2-\frac{3}{2}=\frac{1}{2}\)
Dấu "=" xảy ra khi \(x-1=0\Leftrightarrow x=1\)
:33
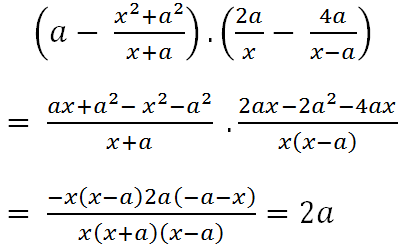 ~~~Học Tốt~~~
~~~Học Tốt~~~



Rút gọn được P = 4a. Do đó P là một số chẵn (vì a nguyên).