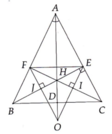
Cho tam giác ABC cân tại A ( A ^ < 90 ° ) , đường phân giác AD. Kẻ đường cao BE, gọi H là giao điểm của BE và AD.
a) Chứng minh C H ⊥ A B .
b) Gọi F là giao điểm của CH và AB. Chứng minh AD là trung trực của EF.
c) Kẻ E I ⊥ H C , F J ⊥ H B với I ∈ H C , J ∈ H B . Chứng minh các đường thẳng EI, FJ,AD cùng đi qua một điểm, kí hiệu điểm đó là O.
d) Chứng minh A C - A F > O F - O C .