Tìm số các số nguyên dương gồm năm chữ số sao cho mỗi chữ số của số đó lớn hơn chữ số ở bên phải nó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 5 2017
Có \(C^5_{10}\) cách chọn 5 chữ số khác nhau để lập số cần thiết. Nhưng khi đã có 5 chữ số khác nhau rồi, chỉ có một cách xếp 5 chữ số đó để tạo nên số cần thiết.
Vậy có \(C^5_{10}=252\) số.
CM
21 tháng 4 2018
Đáp án B
Gọi số cần tìm có dạng a 1 a 2 a 3 a 4 a 5 ¯
thỏa mãn a 1 > a 2 > a 3 > a 4 > a 5
và a 1 ∈ A = 0 ; 1 ; 2 ; . . . ; 9
Vì mỗi tập hợp gồm 5 chữ số thuộc tập hợp A chỉ tạo được một số thỏa yêu cầu bài toán
Vậy có C 10 5 = 252 số cần tìm
CM
31 tháng 10 2019
Đáp án B
Gọi số cần tìm có dạng a 1 a 2 a 3 a 4 a 5 ¯
thỏa mãn a 1 > a 2 > a 3 > a 4 > a 5
và a i ∈ A 0 ; 1 ; 2 ; . . . ; 9
Vì mỗi tập hợp gồm 5 chữ số thuộc tập hợp A chỉ tạo được một số thỏa yêu cầu bài toán
Vậy có C 10 5 = 252 số cần tìm
5 tháng 8 2015
Số có 4 chữ số mà viết theo thứ tự ngược lại vẫn không đổi thì có dạng abba ;
a+b+b+c = 24
hay a + b = 24 : 2 = 12 ( 1 )
và ab – ba = 36
hay 10.a + b – 10.b – a = 36
9.a – 9.b = 36
(a – b) x 9 = 36 => a – b = 36 : 9
a – b = 4 ( 2 )
Từ 1 và 2 ta tìm được số a là:
(12 + 4) : 2 = 8
Số b là: 12 – 8 = 4
Số cần tìm là : 8448
Có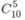
cách chọn 5 chữ số khác nhau để lập số cần thiết. Nhưng khi đã có 5 chữ số khác nhau rồi, chỉ có một cách xếp 5 chữ số đó để tạo nên số cần thiết. Vậy có 
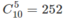số.