Giải các hệ phương trình sau bằng phương pháp thế:
a ) 3 x − 2 y = 11 4 x − 5 y = 3 b ) x 2 − y 3 = 1 5 x − 8 y = 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 6 2018
Bài toán giải hệ phương trình bằng phương pháp thế có 2 cách trình bày.
Cách 1:
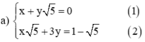
Từ (1) ta rút ra được x = -y√5 (*)
Thế (*) vào phương trình (2) ta được :
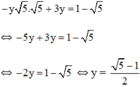
Thay y = 5 - 1 2 vào (*) ta được: x = − 5 − 1 2 ⋅ 5 = 5 − 5 2
Vậy hệ phương trình có nghiệm 5 − 5 2 ; 5 − 1 2
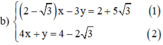
Từ (2) ta rút ra được y = -4x + 4 - 2 √3 (*)
Thế (*) vào phương trình (1) ta được:
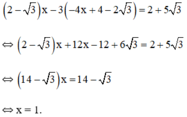
Thay x = 1 vào (*) ta được y = -4.1 + 4 - 2√3 = -2√3
Vậy hệ phương trình có nghiệm duy nhất (1; -2√3)
Cách 2 :
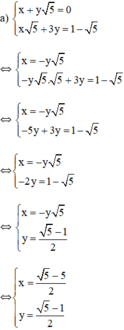
Vậy hệ phương trình có nghiệm duy nhất 5 − 5 2 ; 5 − 1 2
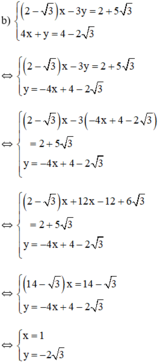
Vậy hệ phương trình có nghiệm duy nhất (1; -2√3)
Kiến thức áp dụng
Giải hệ phương trình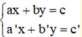 
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
CM
28 tháng 4 2018
Cách 1
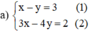
Từ (1) rút ra được y = x – 3
Thế vào phương trình (2) ta được:
3x – 4.(x – 3) = 2 ⇔ 3x – 4x + 12 = 2 ⇔ x = 10
Từ x = 10 ⇒ y = x – 3 = 7.
Vậy hệ phương trình có nghiệm duy nhất (10 ; 7).
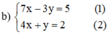
Từ (2) rút ra được y = -4x + 2.
Thế y = -4x + 2 vào phương trình (1) ta được :
7x – 3.(-4x+2) = 5 ⇔ 7x + 12x – 6 = 5 ⇔ 19x = 11 ⇔ x= 11/19
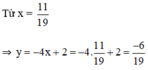
Vậy hệ phương trình có nghiệm duy nhất ( 11/19;-6/19)
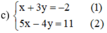
Từ (1) rút x theo y ta được: x = -3y – 2
Thế x = -3y – 2 vào phương trình (2) ta được :
5.(-3y – 2) – 4y = 11 ⇔ -15y – 10 – 4y = 11 ⇔ -19y = 21 ⇔ y = - 21/19
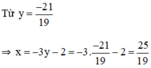
Vậy hệ phương trình có nghiệm duy nhất ( 25/19; -21/19)
Cách 2
Kiến thức áp dụng
Giải hệ phương trình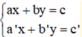 
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn)..
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương ..
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
PT
1
CM
27 tháng 4 2017
x - y = 3 3 x - 4 y = 2
Từ (1) rút ra được y = x – 3
Thế vào phương trình (2) ta được:
3x – 4.(x – 3) = 2 ⇔ 3x – 4x + 12 = 2 ⇔ x = 10
Từ x = 10 ⇒ y = x – 3 = 7.
Vậy hệ phương trình có nghiệm duy nhất (10 ; 7).
CM
6 tháng 9 2019
Cách 1
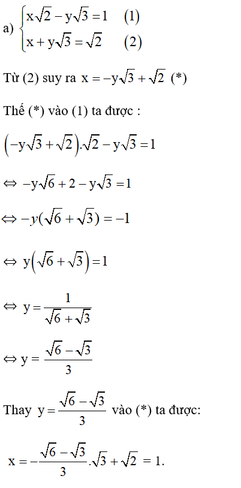
Vậy hệ phương trình có nghiệm duy nhất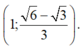 
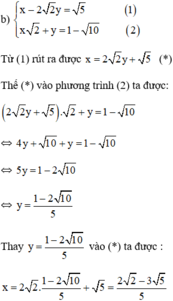
Vậy hệ phương trình có nghiệm duy nhất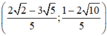 
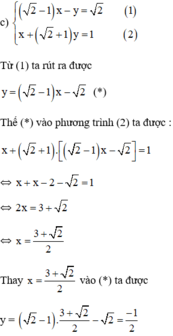
Vậy hệ phương trình có nghiệm duy nhất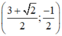 
Cách 2
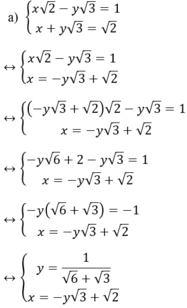
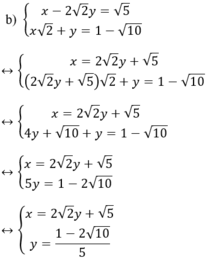
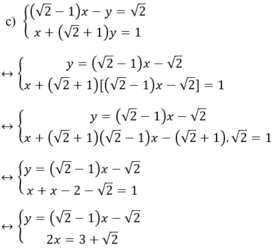
Kiến thức áp dụng
Giải hệ phương trình ta làm như sau:
Bước 1: Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
HP
18 tháng 1 2021
Làm mẫu hai câu a, b thôi nha.
a, \(\left\{{}\begin{matrix}x-\sqrt{3}y=0\\\sqrt{3}x+2y=1+\sqrt{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{3}y\\\sqrt{3}.\sqrt{3}y+2y=1+\sqrt{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{3}y\\5y=1+\sqrt{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\sqrt{3}+3}{5}\\y=\dfrac{1+\sqrt{3}}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\approx0,95\\y\approx0,55\end{matrix}\right.\)
b, \(\left\{{}\begin{matrix}\sqrt{2}x-\sqrt{5}y=1\\x+\sqrt{5}y=\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{2}\left(\sqrt{2}-\sqrt{5}y\right)-\sqrt{5}y=1\\x=\sqrt{2}-\sqrt{5}y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2-\sqrt{5}\left(\sqrt{2}+1\right)y=1\\x=\sqrt{2}-\sqrt{5}y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{\sqrt{2}-1}{\sqrt{5}}\\x=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y\approx0,19\\x=1\end{matrix}\right.\)
T
18 tháng 1 2021
a) \(\left\{{}\begin{matrix}x-\sqrt{3}y=0\\\sqrt{3}x+2y=1+\sqrt{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{3}x-3y=0\\\sqrt{3}x+2y=1+\sqrt{3}\end{matrix}\right.\)
Lấy phương trình dưới trừ phương trình trên thu được: \(5y=1+\sqrt{3}\Rightarrow y=\dfrac{1+\sqrt{3}}{5}\Rightarrow x=\sqrt{3}y=\dfrac{3+\sqrt{3}}{5}\)
b) Cộng hai phương trình lại với nhau thu được:
\(\left(\sqrt{2}+1\right)x=\sqrt{2}+1\Leftrightarrow x=1\Rightarrow y=\dfrac{\sqrt{2}-1}{\sqrt{5}}\)
c) \(\left\{{}\begin{matrix}\sqrt{2}x+\sqrt{5}y=2\\x+\sqrt{5}y=2\end{matrix}\right.\)
Lấy phương trình trên trừ phương trình dưới:
\(\left(\sqrt{2}-1\right)x=0\Leftrightarrow x=0\Rightarrow y=\dfrac{2-x}{\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)
d) Hướng dẫn. Nhân phương trình đầu với \(\sqrt{2}\) rồi lấy phương trình thu được trừ phương trình dưới.
PT
1
16 tháng 9 2023
=>4x+4y+y=6 và 3x+3y+y=8
=>4x+5y=6 và 3x+4y=8
=>12x+15y=18 và 12x+16y=32
=>-y=-14 và 4x+5y=6
=>y=14 và 4x=6-5y=6-70=-64
=>x=-16 và y=14
LQ
0
Bài toán giải hệ phương trình bằng phương pháp thế có 2 cách trình bày.
Cách 1:
Từ (1) ta rút ra được y = 3 2 x − 11 2 (*)
Thế (*) vào phương trình (2) ta được :
Thay x = 7 vào (*) ta suy ra y = 3 2 ⋅ 7 − 11 2 = 5
Vậy hệ phương trình có nghiệm duy nhất (7 ; 5).
Từ (1) ta rút ra được : y = 3 2 x − 3 (*)
Thế (*) vào phương trình (2) ta được :
Thay x = 3 vào (*) ta suy ra
Vậy hệ phương trình có nghiệm duy nhất (3; 3/2)
Cách 2:
Vậy hệ phương trình có nghiệm duy nhất (7; 5).
Vậy hệ phương trình có nghiệm duy nhất (3; 3/2)
Kiến thức áp dụng
Giải hệ phương trình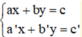
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.