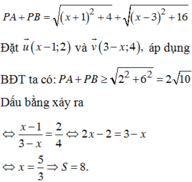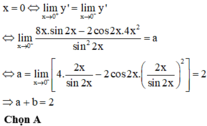tính tổng các số nguyên x thỏa mãn điều kiện :khoảng cách từ điểm x đến điểm 0 trên trục số nhỏ hơn 2021
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\left|x+1\right|+\left|y-2\right|+5\ge5\)
Dấu ''='' xảy ra khi x = -1 ; y = 2
Vậy ...


Lời giải:
$|x+2|+2|x+2|=3$
$3|x+2|=3$
$|x+2|=1$
$\Rightarrow x+2=1$ hoặc $x+2=-1$
$\Rightarrow x=-1$ hoặc $x=-3$
Vậy có 2 giá trị nguyên của $x$ thỏa mãn
Đáp án C.

\(=\left|1-x\right|+\left|x+2\right|-3\ge\left|1-x+x+2\right|-3=0\)
Dấu ''='' xảy ra khi \(\left(1-x\right)\left(x+2\right)\ge0\Leftrightarrow-2\le x\le1\)
mà x là số nguyên nên x = -2 ; -1 ; 0 ; 1

(x+8)(x-4) ≤ 0
⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x+8\le0\\x-4\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x+8\ge0\\x-4\le0\end{matrix}\right.\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\le-8\\x\ge4\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge-8\\x\le4\end{matrix}\right.\end{matrix}\right.\)⇔ \(\left\{{}\begin{matrix}x\ge-8\\x\le4\end{matrix}\right.\)
SSH= = \(\dfrac{4-\left(-8\right)}{1}+1\) = 13
S=(số đầu + số cuối) . \(\dfrac{SSH}{2}\)= (-8+4) . \(\dfrac{13}{2}\)= -26
Vậy ........