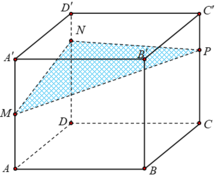
Cho khối hộp chữ nhật ABCD. A'B'C'D' có thể tích bằng 2110. Biết (MNP), DN=3ND', CP=2C'P như hình vẽ. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằng:
A. 5275 6
B. 8440 9
C. 7485 18
D. 5275 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Cho lăng trụ A B C D . A ' B ' C ' D ' có A M = a , B N = b , C P = c , S = S A B C .
Khi đó V M N P . A B C = a + b + c 3 . S
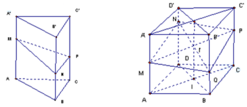
Đặt A A ' = a ⇒ A M = a 2 , P C = 2 a 3 ;
Ta có D N + B Q = 2 I I ' = M A + P C = 7 a 6 ; S A B D = S C B D = S
Áp dụng tính chất có
V M N P Q . A B C D = V M N P . A D B + V N Q P . C B C = 1 3 A M + B Q + D N . S + 1 3 D N + B Q + C P . S = 1 3 3 A M + 3 P C . S = 7 6 a . S = 7 12 V A B C D . A ' B ' C ' D ' ⇒ V A ' B ' C ' D ' . M N P Q = 5 12 V A B C D . A ' B ' C ' D ' = 5 12 .2018 = 5045 6

Đáp án A.
Ta chứng minh được công thức tỷ số thể tích tối với khối hộp như sau (học sinh có thể tự chứng minh).
V A ' B ' C ' D ' . M N P Q V A ' B ' C ' D ' . A B C D = 1 2 A ' M A ' A + C ' P C ' C = 1 2 B ' Q B ' B + D N D ' D = 7 2
Do đó thể tích khối đa diện nhỏ hơn là 15 2 V = 5 2 .2018 = 5045 6 .
Chọn A
Gọi Q là giao điểm của mặt phẳng (MNP) với BB'.