Một mẫu U238 có khối lượng 1 (g) phát ra 12400 hạt anpha trong một giây. Tìm chu kì bán rã của đồng vị này. Coi một năm có 365 ngày, số avogadro là 6 ٫ 023 . 10 23 .
A. 4,4 (tỉ năm).
B. 4,5 (tỉ năm).
C. 4,6 (tỉ năm).
D. 0,45 (tỉ năm).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Số hạt U238 đã phân rã bằng số hạt alpha tạo thành:
Thời gian rất ngắn nên
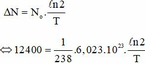
![]() ≈ 4,5 tỉ năm.
≈ 4,5 tỉ năm.

Chọn đáp án C
Khối lượng hạt nhân con ở thời điểm t.
Δ N = N c o n = N 0 1 − 2 − 1 T ⇔ m c o n A c o n . N A ⏟ N c o n = m 0 A m e . N A ⏟ N 0 1 − 2 − 1 T
⇒ m c o n = m 0 A c o n A m e 1 − 2 − 1 T (Học thuộc).
Áp dụng công thức ở trên ta được: 0 , 2 = m 0 . 206 238 1 − 2 − 2 4.47 → S H I F T − S O L V E m 0 = 0 , 866557...
Làm tròn đến chữ số thập phân thứ 3 thì m 0 = 0 , 867 g

Đáp án C
Phương pháp:D Áp dụng công thức tính khối lượng chất mới sinh ra

Cách giải: Chọn C
Khối lượng Pb được tạo thành:
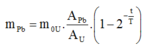
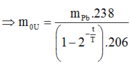


Chọn đáp án C
Số hạt nhân con ở thời điểm t:


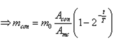
Áp dụng công thức ở trên ta được:

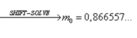
*Làm tròn đến chữ số thập phân thứ 3 thì
![]()
Đáp án B