Cho hình chóp S.ABC có đáy là tam giác cân ABC cân tại C. Gọi I là trung điểm của AB. Biết SA = SB và SAB ⊥ ABC . Khẳng định nào sau đây là sai?
A. SI ⊥ SAB .
B. IC ⊥ SAB .
C. SAC = SAB
D. SC ⊥ SAB .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có S A = S B và C A = C B nên Δ S A C = Δ S B C
Ta có I C ⊥ A B A B C ⊥ S A B suy ra I C ⊥ S A B
Chứng minh tương tự ta có S I ⊥ A B C
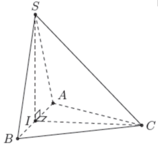

Đáp án D

Khẳng định D sai, khẳng định A,B,C đúng vì ta có AH ⊥ (SAB).

Đáp án D
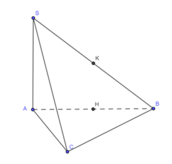
Khẳng định D sai, khẳng định A,B,C đúng vì ta có A H ⊥ S A B

Đáp án B
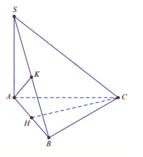
Vì ∆ A B C cân tại C và H là trung điểm của AB nên C H ⊥ A B .
Mà S A ⊥ A B C ⇒ S A ⊥ C H ⇒ C H ⊥ S A B ⇒ C H ⊥ S A C H ⊥ S B C H ⊥ A K ⇒
Các khẳng định A,C và D đúng. Khẳng định B sai.

Đáp án A
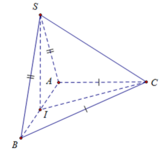
Ta có tam giác SAB cân tại A,I là trung điểm A B ⇒ S I ⊥ A B
Lại có S A B ⊥ A B C ⇒ S I ⊥ A B C ⇒ Góc giữa đường thẳng và mặt phẳng (ABC) là: S C I ⏜ .
Đáp án D