Tính:
57 hm – 28 hm =
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 11 2019
8 dam + 5 dam = 13 dam
57 hm – 28 hm = 29 hm
12 km x 4 = 48 km
DN
2
12 tháng 8 2023
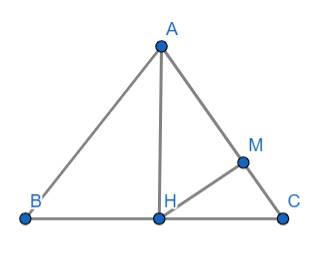
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=7/2=3,5
\(AH=\sqrt{AB^2-HB^2}=\dfrac{7\sqrt{3}}{2}\)
b: Xét ΔAHC vuông tại H có HM là đường cao
nên HM*AC=AH*HC
=>HM*7=7/2*căn 3*3,5=49/4*căn 3
=>HM=7/4*căn 3
AM=AH^2/AC=21/4
CM=7-21/4=7/4
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 6 2021
Kí hiệu \(P_{AMN}\) ở đây nghĩa là gì em nhỉ? Chắc là chu vi tam giác?
Tứ giác AMHN là hình chữ nhật (có 3 góc vuông) \(\Rightarrow\widehat{BAH}=\widehat{AMN}\)
Mà \(\widehat{BAH}=\widehat{ACB}\) (cùng phụ \(\widehat{ABC}\))
\(\Rightarrow\widehat{AMN}=\widehat{ACB}\)
\(\Rightarrow\Delta_vAMN\sim\Delta_VACB\) (g.g)
\(\Rightarrow\dfrac{AM}{AC}=\dfrac{AN}{AB}=\dfrac{MN}{BC}=\dfrac{AM+AN+MN}{AC+AB+BC}=\dfrac{14}{28}=\dfrac{1}{2}\)
Mà \(MN=AH\) (hai đường chéo hình chữ nhật)
\(\Rightarrow BC=2AH\)
Gọi K là trung điểm BC \(\Rightarrow BC=2AK\) (trung tuyến ứng với cạnh huyền bằng 1 nửa cạnh huyền)
\(\Rightarrow\) H trùng K \(\Rightarrow AH\) vừa là đường cao vừa là trung tuyến
\(\Rightarrow\Delta ABC\) vuông cân tại A
\(\Rightarrow\widehat{ABC}=45^0\)
H9
HT.Phong (9A5)
CTVHS
12 tháng 8 2023
AH là đường cao mà tam giác ABC là tam giác đều nên AH đồng thời là đương trung tuyến
\(\Rightarrow H\) là trung điểm của BC
\(\Rightarrow HB=HC=\dfrac{BC}{2}=\dfrac{7}{2}=3,5\left(cm\right)\)
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow AH=\sqrt{\dfrac{AB^2AC^2}{AB^2+AC^2}}=\sqrt{\dfrac{7^2\cdot7^2}{7^2+7^2}}=\dfrac{7\sqrt{2}}{2}\left(cm\right)\)
Xét tam giác AHC có HM là đường cao ta có:
\(\dfrac{1}{HM^2}=\dfrac{1}{AH^2}+\dfrac{1}{HC^2}\)
\(\Rightarrow HM=\sqrt{\dfrac{AH^2HC^2}{AH^2+HC^2}}=\sqrt{\dfrac{\left(\dfrac{7\sqrt{2}}{2}\right)^2\cdot3,5^2}{\dfrac{7\sqrt{2}}{2}+3,5}}=\dfrac{7\sqrt{6}}{6}\left(cm\right)\)
Xét tam giác AHM vuông tại M áp dụng định lý Py-ta-go ta có:
\(AH^2=HM^2+AM^2\)
\(\Rightarrow AM=\sqrt{AH^2-HM^2}=\sqrt{\left(\dfrac{7\sqrt{2}}{2}\right)^2-\left(\dfrac{7\sqrt{6}}{6}\right)^2}=\dfrac{7\sqrt{3}}{3}\left(cm\right)\)
Mà: \(AM+MC=AC\)
\(\Rightarrow MC=AC-AM=7-\dfrac{7\sqrt{3}}{3}=\dfrac{21-7\sqrt[]{3}}{3}\)
TB
1
31 tháng 8 2021
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2.4\left(cm\right)\\CH=3.2\left(cm\right)\end{matrix}\right.\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔACH vuông tại H có HM là đường cao ứng với cạnh huyền AC, ta được:
\(\left\{{}\begin{matrix}HM\cdot AC=AH\cdot HC\\CH^2=CM\cdot CA\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}HM=1.92\left(cm\right)\\CM=2.56\left(cm\right)\end{matrix}\right.\)
MX
10
10 tháng 4 2017
795g = 0,795 kg
26 kg = 0,26 tạ
105 m = 1,05 hm
5 x 7 = 35
57 + 0 = 57
74 + 1 = 75tk mk nha mk tk bạn cả ngày rồi đó !
57 hm – 28 hm = 29 hm