Nêu định nghĩa hàm liên tục tại một điểm, trên một khoảng. Nêu nhận xét về đồ thị của một hàm số liên tục trên một khoảng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


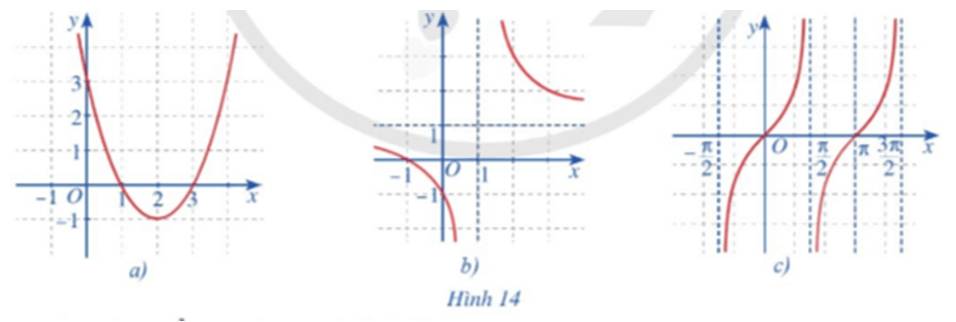
Hình 14a đồ thị là đường cong Parabol liền mạch nên hàm số liên tục trên toàn bộ trên khoảng xác định.
Hình 14b đồ thị bị chia làm hai nhánh:
- Với x < 1 ta thấy hàm số là một đường cong liền nên liên tục.
- Với x > 1 ta thấy hàm số là một đường cong liền nên liên tục.
Vậy hàm số liên tục trên từng khoảng xác định.
Hình 14c đồ thị hàm số y = tanx chia thành nhiều nhánh, và mỗi nhánh là các đường cong liền. Do đó hàm số liên tục trên mỗi khoảng xác định của chúng.

a) Đồ thị hàm số (hình bên).
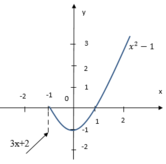
Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
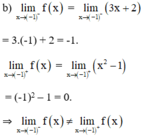
⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.

a) Các bạn tự vẽ hình nhé . Đồ thị hàm số y = f(x) là một đường không liền nét mà bị đứt quãng tại x0 = -1. Vậy hàm số đã cho liên tục trên khoảng (-∞; -1) và (- 1; +∞).
b) +) Nếu x < -1: f(x) = 3x + 2 liên tục trên (-∞; -1) (vì đây là hàm đa thức).
+) Nếu x> -1: f(x) = x2 – 1 liên tục trên (-1; +∞) (vì đây là hàm đa thức).
+) Tại x = -1;
Ta có =![]() = 3(-1) +2 = -1.
= 3(-1) +2 = -1.
![]() = (-1)2 – 1 = 0.
= (-1)2 – 1 = 0.
Vì ![]() nên không tồn tại
nên không tồn tại  . Vậy hàm số gián đoạn tại
. Vậy hàm số gián đoạn tại
x0 = -1.

Chọn A.
Tập xác định của hàm số y = f(x) là D =
ℝ
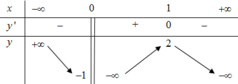
. Từ đồ thị đã cho ta có: 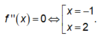
Bảng biến thiên
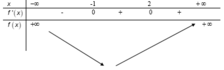
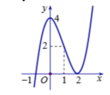
Dựa vào bảng biến thiên của hàm số ta nhận thấy hàm số y = f(x) đồng biến trên khoảng (-1;+ ∞ )

Chọn B
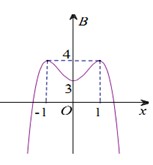
Phương pháp: Dùng kiến thức cực đại cực tiểu của hàm số
Cách giải:
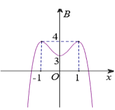
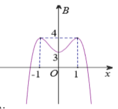
Nhìn vào đồ thị, ta thấy hàm số đạt cực tiểu tại điểm có tọa độ (0; 3)

Đáp án A.
Hàm số có y = x4 – x + 2 không là hàm số chẵn nên mệnh đề I sai.
Mệnh đề II, III, IV đúng

+ Hàm số liên tục tại một điểm
+ Hàm số liên tục trên một khoảng
- Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó.
- Hàm số y = f(x) được gọi là liên tục trên một đoạn [a; b] nếu nó liên tục tại mọi điểm thuộc khoảng (a;b) và
Đồ thị của hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó.