Cho đường tròn (O), đường kính AD = 2R. Vẽ cung tròn tâm D bán kính R, cung này cắt (O) ở B và C
a, Tứ giác OBDC là hình gì? Vì sao?
b, Tính số đo các góc C B D ^ ; C B O ^ ; O B A ^
c, Chứng minh tam giác ABC là tam giác đều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

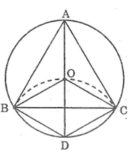
Ta có:
OB = OC = R (vì B, C nằm trên (O; R))
DB = DC = R (vì B, C nằm trên (D; R))
Suy ra: OB = OC = DB = DC
Vậy tứ giác OBDC là hình thoi

a: Xét tứ giác OBDC có OB=BD=DC=OC=R
nên OBDC là hình thoi
b: Xét ΔOBD có OB=OD=BD(=R)
nên ΔOBD đều
=>\(\widehat{OBD}=60^0\)
OBDC là hình thoi
=>\(\widehat{OCD}=\widehat{OBD}=60^0\)
OBDC là hình thoi
=>\(\widehat{BOC}+\widehat{OBD}=180^0\)
=>\(\widehat{BOC}=180^0-60^0=120^0\)
OBDC là hình thoi
=>\(\widehat{BOC}=\widehat{BDC}=120^0\)
OBDC là hình thoi
=>BC là phân giác của góc OBD
=>\(\widehat{CBD}=\widehat{CBO}=\dfrac{\widehat{OBD}}{2}=\dfrac{60^0}{2}=30^0\)
Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>\(\widehat{ABD}=90^0\)
\(\widehat{ABO}+\widehat{OBD}=\widehat{ABD}\)
=>\(\widehat{ABO}+60^0=90^0\)
=>\(\widehat{ABO}=30^0\)
c: Gọi giao điểm của OD và BC là H
OBDC là hình thoi
=>OD vuông góc với BC tại trung điểm của mỗi đường
=>OD\(\perp\)BC tại H và H là trung điểm chung của OD và BC
\(\widehat{ABC}=\widehat{ABO}+\widehat{CBO}=30^0+30^0=60^0\)
Xét ΔABC có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABC cân tại A
Xét ΔABC cân tại A có \(\widehat{ABC}=60^0\)
nên ΔABC đều

a) Ta có:
OB = OC = R (vì B, C nằm trên (O ; R))
DB = DC = R ( vì B, C nằm trên (D ; R))
Suy ra : OB = OC = DB = DC.
Vậy tứ giác OBDC là hình thoi.
b) Ta có: OB = OD = BD = R
∆OBD đều ⇒ˆOBD=60∘
Vì OBDC là hình thoi nên:
ˆCBD=ˆOBC=12ˆOBD=30∘CBD^=OBC^=12OBD^=30∘
Tam giác ABD nội tiếp trong (O) có AD là đường kính nên:
ˆABD=90∘ABD^=90∘
Mà ˆOBD+ˆOBA=90∘OBD^+OBA^=90∘
Nên ˆOBA=ˆABD–ˆOBD=90∘–60∘=30∘OBA^=ABD^–OBD^=90∘–60∘=30∘
c) Tứ giác OBDC là hình thoi nên OD ⊥ BC hay AD ⊥ BC
Ta có: AB = AC ( tính chất đường trung trực)
Suy ra tam giác ABC cân tại A (1)
Mà ˆABC=ˆOBC–ˆOBA=30∘+30∘=60∘ABC^=OBC^–OBA^=30∘+30∘=60∘. (2)
Từ (1) và (2) suy ra tam giác ABC đều.
a, HS Tự chứng minh
b, Tính được C B D ^ = C B O ^ = O B A ^ = 30 0
c, Chứng minh ∆ABC cân tại A có: A B C ^ = 60 0 => ∆ABC đều