Cho hàm số f(x) = cos 2x và g(x) = tan 3x, chọn mệnh đề đúng
A. f(x) là hàm số chẵn, g(x) là hàm số lẻ
B. f(x)là hàm số lẻ, g(x) là hàm số chẵn.
C. f(x)là hàm số lẻ, g(x) là hàm số chẵn
D. f(x) và g(x) đều là hàm số lẻ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
24 tháng 11 2019
Đúng(0)
Những câu hỏi liên quan
CM
1 tháng 8 2019
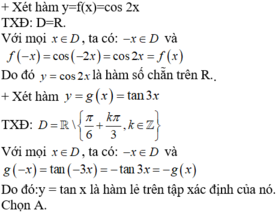
Đáp án D
a, Xét hàm số f ( x ) = 1 x - 3 + 3 sin 2 x có tập xác định là D = R\{3}.
Ta có x = -3 ∈ D nhưng -x = 3 ∉ D nên D không có tính đối xứng. Do đó ta có kết luận hàm số f(x) không chẵn không lẻ.
b, Xét hàm số g ( x ) = sin 1 - x có tập xác định là D2 = [1; + ∞). Dễ thấy D2 không phải là tập đối xứng nên ta kết luận hàm số g(x) không chẵn không lẻ.
CM
26 tháng 8 2017
Tập xác định của hàm số f(x)và g(x) đều là ℝ .
Với x ∈ ℝ thì - x ∈ ℝ và ta có: f - x = - - x = - x = f x ;
g - x = - x + 1 - - x - 1 = x - 1 - x + 1 = - g x .
Vậy f(x)là hàm số chẵn, g(x) là hàm số lẻ. Đáp án là D.