Cho hàm số y = - 4 x 3 + 4 x . Để y ' ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây ?
A. - 3 ; 3
B. - 1 3 ; 1 3
C. ( - ∞ ; - 3 ] ∪ [ 3 ; + ∞ )
D. ( - ∞ ; - 1 3 ] ∪ [ 1 3 ; + ∞ )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Ta có: y = (2x2 + 1)3 ⇒ y’ = 12x(2x2 + 1)2 ⇒ y’ ≥ 0 ⇔ x ≥ 0.

Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)

Vẽ hình:
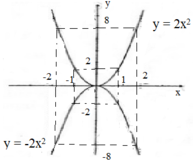
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.

a: \(y=-x^2+2x+3\)
y>0
=>\(-x^2+2x+3>0\)
=>\(x^2-2x-3< 0\)
=>(x-3)(x+1)<0
TH1: \(\left\{{}\begin{matrix}x-3>0\\x+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>3\\x< -1\end{matrix}\right.\)
=>\(x\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}x-3< 0\\x+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 3\\x>-1\end{matrix}\right.\)
=>-1<x<3
\(y=\dfrac{1}{2}x^2+x+4\)
y>0
=>\(\dfrac{1}{2}x^2+x+4>0\)
\(\Leftrightarrow x^2+2x+8>0\)
=>\(x^2+2x+1+7>0\)
=>\(\left(x+1\right)^2+7>0\)(luôn đúng)
b: \(y=-x^2+2x+3< 0\)
=>\(x^2-2x-3>0\)
=>(x-3)(x+1)>0
TH1: \(\left\{{}\begin{matrix}x-3>0\\x+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>3\\x>-1\end{matrix}\right.\)
=>x>3
TH2: \(\left\{{}\begin{matrix}x-3< 0\\x+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 3\\x< -1\end{matrix}\right.\)
=>x<-1
\(y=\dfrac{1}{2}x^2+x+4\)
\(y< 0\)
=>\(\dfrac{1}{2}x^2+x+4< 0\)
=>\(x^2+2x+8< 0\)
=>(x+1)2+7<0(vô lý)
Chọn B
Ta có
y = - 4 x 3 + 4 x ⇒ y ' = - 12 x 2 + 4
nên
y ' ≥ 0 ⇔ − 12 x 2 + 4 ≥ 0 ⇔ x 2 ≤ 1 3 ⇔ x ∈ − 1 3 ; 1 3