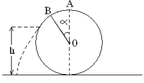
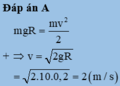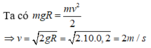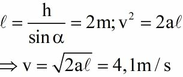Một vật trượt không ma sát trên một rãnh có dạng như hình vẽ, từ độ cao h=5R ( với R là bán kính vòng tròn)so với mặt phẳng nằm ngang và không có vận tốc đầu. Tính: a. Vận tốc của vật tại điểm thấp nhất. b. Vận tốc tại thời điểm cao nhất của vật tại điểm cao nhất.
của vật tại điểm cao nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
Tại điểm cao nhất của vòng tròn ta có m v 2 R = N + P ⇒ N = m v 2 R − P ( 1 )
Áp dụng định luật bảo toàn cơ năng cho hai vị trí đó là khi vật ở vị trí có độ cao h và khi vật ở vị trí cao nhất trên vòng tròn m g h = 1 2 m v 2 + m g .2 R ⇒ v 2 = 2 g h − 2 R → 1 N = 2 m g h − 2 R R − m g
Vật không rời tại điểm cao nhất trên vòng tròn khi
N ≥ 0 ⇔ 2 m g h − 2 R R − m g ≥ 0 ⇒ h ≥ 5 R 2 ⇒ h min = 5 R 2
Chú ý: Đối với bài toán hỏi áp lực tại các điểm cao nhất và thấp nhất trên vòng tròn chúng ta chỉ cần tìm độ lớn của phản lực thì suy ra độ lớn áp lực bằng độ lớn phản lực.

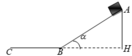
Chọn mốc thế năng tại mặt nằm ngang BC
Theo định luật bảo toàn năng lượng
W A = W C + A m s
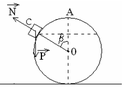
Mà W A = m g . A H = m .10 = 10. m ( J ) ; W C = 0 ( J ) A m s = μ m g cos α . A B + μ m g . B C = 0 , 1. m .10. cos 30 0 . A H sin 30 0 + 0 , 1. m .10. B C ⇒ A m s = m . 3 . + m . B C ⇒ 10. m = 0 + m 3 + m . B C ⇒ B C = 8 , 268 ( m )

a, Khi vật đang ở A, động năng của vật là cực đại và nó bằng thế năng của vật tại B (Wt max):
Wtmax = mgz = 4 . 10 . 0,8 = 32 (J)
⇒ \(\dfrac{1}{2}mv^2=32\)
⇒ v = 4 (m/s)
Vậy khi đến B v = 4 m/s
b, Do có lực ma sát nên cơ năng không được bảo toàn
Độ biến thiên cơ năng bằng công của lực ma sát
Tại B, cơ năng của vật là
W = Wđmax = 32 (J)
Tại C cơ năng của vật là
W = Wt + Wđ = 40. BC
Ta có 40BC - 32 = F . BC
⇒ 40BC - 32 = N . 0.25 . BC
⇒ 40BC - 32 = 10BC
⇒ BC = \(\dfrac{32}{30}=1,06\left(m\right)\)

Chon mốc thế năng tại mặt đất. Theo định luật bảo toàn cơ năng
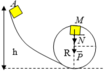
W A = W M ⇒ m g h = 1 2 m v M 2 + m g z M ⇒ 1 2 m . v M 2 = m g ( h A − 2 R ) ( 1 )
Mặt ta có :
P + N = m v M 2 R ⇒ N = m v M 2 R − m g
Để vật vẫn chuyển động trên vòng thì N ≥ 0
⇒ m v M 2 R − m g ≥ 0 ⇒ 1 2 m v M 2 ≥ m g R 2 ( 2 )
Từ ( 1 ) và ( 2 ) ta có
m g ( h − 2 R ) ≥ m g R 2 ⇒ h ≥ 2 R + R 2 = 5 R 2
Nếu R = 20cm thì chiều cao là
⇒ h ≥ 5.0 , 2 2 = 0 , 5 m = 50 c m
b. Từ ( 1 ) ta có
⇒ 1 2 m . v M 2 = m g ( h A − 2 R ) ⇒ v M = 2 g ( h − 2 R ) ⇒ v M = 2.10 ( 0 , 6 − 2.0 , 2 ) = 2 ( m / s )