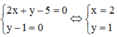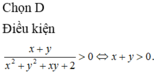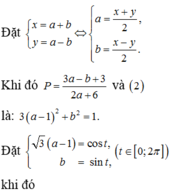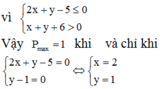Cho biểu thức: K = 2 x 3 y xy 2 x - 3 y - 6 - 6 - xy...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

PT

Pham Trong Bach

13 tháng 12 2019

Cho biểu thức: K = 2 x + 3 y xy + 2 x - 3 y - 6 - 6 - xy xy + 2 x + 3 y + 6 A. K = x + 9 x - 9 B. K = x - 9 x + 9 C. K = x + 9 x - ...

1

CM

Cao Minh Tâm

13 tháng 12 2019

Những câu hỏi liên quan

PH

Phan Hà Phương

29 tháng 8 2015 - olm

1. Phân tích đa tức thành nhân tử: (x-2)(x-4)(x-6)(x-9)+15

2. Tính giá trị biểu thức sau, biết x^3 -x=6. A=x^6 -2x^4 +x^3 +x^2 -x

3.Cho x, y là 2 số khác nhau thỏa manc: x^2 +y=y^2 +x. Tính giá trị biểu thức sau A= (x^2 +y^2 +xy) : (xy-1)

0

PD

Phan Đại Dương (N.N.D) 7A THCS AnTh...

1 tháng 1 2020 - olm

Rút gọn biểu thức:

K= \((x^2y-3)^2-(2x-y)^3+xy^2(6-x^3)+8x^3-6x^2y-y^3\)

1

LT

Lê Tài Bảo Châu

2 tháng 1 2020

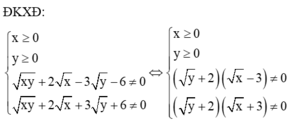
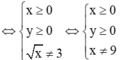
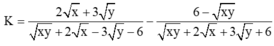
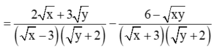
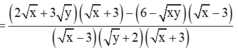
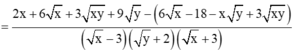
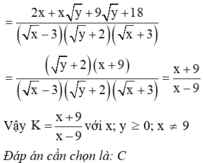
\(K=\left(x^2y-3\right)^2-\left(2x-y\right)^3+xy^2\left(6-x^3\right)+8x^3-6x^2y-y^3\)

\(=x^4y^2-6x^2y+9-4x^2+4xy-y^2+6xy^2-x^4y^2+8x^3-6x^2y-y^3\)

\(=-12x^2y+9-4x^2+4xy-y^2+6xy^2+8x^3-y^3\)

PT

Pham Trong Bach

15 tháng 11 2018

Cho hai số thực x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x x - 3 + y y - 3 + x y . Tìm giá trị lớn nhất của biểu thức P = x + 2 y + 3 x + y + 6 ...

#Toán lớp 12

1

CM

Cao Minh Tâm

15 tháng 11 2018

PP

Phươngg Phương

29 tháng 8 2015 - olm

1. Tính Giá trị nhỏ nhất của biểu thứ (x+1)(x+2)(x+3)(x+6)+2010
2. Phân tích đa thức thành nhân tử (x-2)(x-4)(x-6)(x-8) +15
3. Tính giá trị biểu thức sau: x^2 +y= y^2 +x. tính giá trị của biểu thức sau A= (x^2 +y^2 +xy) : (xy-1)

1

NN

Nguyễn Ngọc Bảo Ngân

30 tháng 12 2020

bbgfhfygfdsdty64562gdfhgvfhgfhhhhh

\hvhhhggybhbghhguyg

HP

Hữu Phúc Phạm

14 tháng 5 2022

Câu 2: (1,5 điểm) Hãy thu gọn các đơn thức,đa thức sau:
a) A = - ( 6 . 8 x x 7 6 3 y y ) ( 3 )
b) B xy xy xy xy = - - + + + 7 2 8 5 6

0

TB

Trần Bảo Ngọc Hòa

12 tháng 11 2019 - olm

tính biểu thức cho x-y=-5, xy=-6

x³-y³-x²+2xy-y²

1

KN

Kiệt Nguyễn

12 tháng 11 2019

\(x^3-y^3-x^2+2xy-y^2\)

\(=\left(x-y\right)\left(x^2+xy+y^2\right)-\left(x-y\right)^2\)

\(=5\left[\left(x-y\right)^2+3xy\right]-5^2\)

\(=5\left[5^2+3.\left(-6\right)\right]-25\)

\(=5\left[25-18\right]-25\)

\(=5.7-25=35-25=10\)

TN

Trần Nguyên Đán

4 tháng 5 2020 - olm

Cho x>0, y>0 thỏa mãn xy=6. Tìm GTNN của biểu thức Q= 2/x +3/y + 6/3x+2y

0

PT

Pham Trong Bach

6 tháng 2 2019

Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x(x - 3) + y(y - 3) + xy. Tìm giá trị Pmax của biểu thức P = 3 x + 2 y + 1 x + y + 6 A. Pmax = 0 B. Pmax = 2 C. Pmax = 1 D. Pmax =...

1

CM

Cao Minh Tâm

6 tháng 2 2019

Đáp án C

Phương pháp:

- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.

Cách giải:

<=>

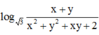
(2)

Đặt

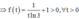
=> f(t) đồng biến trên (0;+∞)

<=>

<=>

Khi đó,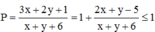

vì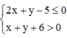

Vậy P_max = 1 khi và chỉ khi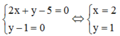

PT

Pham Trong Bach

14 tháng 4 2019

Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y Tìm giá trị P m a x của biểu thức P = 3 x + 2 y + 1 x + y + 6 . ...

#Toán lớp 12

1

CM

Cao Minh Tâm

14 tháng 4 2019

PT

Pham Trong Bach

13 tháng 9 2019

Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y . Tìm giá trị Pmax của biểu thức P = 3 x + 2 y + 1 x + y + 6 A. Pmax = 0...

1

CM

Cao Minh Tâm

13 tháng 9 2019

Đáp án C

Phương pháp giải:

- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.

Lời giải:

log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y (1)

(2)

Đặt

=> f(t) đồng biến trên (0;+∞)

Khi đó,

vì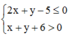

Vậy P_max = 1 khi và chỉ khi