Thu gọn biểu thức x 3 + 3 x 2 + 3 x + 1 3 - 8 x 3 + 12 x 2 + 6 x + 1 3 ta được
A. x
B. –x
C. 2x
D. −2x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

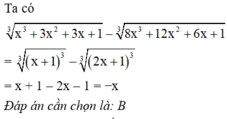

a: =18x^3y^2-12x^3y^3+6x^2y^2
b: (-3x+2)(5x^2-1/3x+4)
=-12x^3+x^2-12x+10x^2-2/3x+8
=-12x^3+11x^2-38/3x+8
c: =x^2-x-2+3x-x^2
=2x-2
d: =4x^2+12x+9-4x^2+25-(x-1)(x^2+12)
=12x+34-x^3-12x+x^2+12
=-x^3+x^2+46

a: Trường hợp 1: x<-1
A=3(-x-1)+2(-x+3)+2x-5
=-3x-3-2x+6+2x-5
=-3x-2
Trường hợp 2: -1<=x<3
A=3(x+1)+2(3-x)+2x-5
=3x+3+6-2x+2x-5
=3x+4
Trường hợp 3: x>=3
A=3(x+1)+2(x-3)+2x-5
=3x+3+2x-6+2x-5
=7x-8
b: Trường hợp 1: x<-7
B=-x-7+2(3-x)-x-4
=-2x-11+6-2x=-4x-5
TRường hợp 2: -7<=x<3
B=x+7+2(3-x)-x-4
=3+6-2x=-2x+9
Trường hợp 3: x>=3
B=x+7+2x-6-x-4=2x-3
c: Trường hợp 1: x<1
C=8(1-x)+2(3-x)-5x-3
=8-8x+6-2x-5x-3
=-15x+11
Trường hợp 2: 1<=x<3
C=8(x-1)+2(3-x)-5x-3
=8x-8+6-2x-5x-3
=x-5
TRường hợp 3: x>=3
C=8(x-1)+2(x-3)-5x-3
=8x-8+2x-6-5x-3
=5x-17

a: Trường hợp 1: x<-1
A=2(3-x)+3(-x-1)+2x-5
=6-2x-3x-3+2x-5
=-3x-2
Trường hợp 2: -1<=x<3
A=2(3-x)+3(x+1)+2x-5
=6-2x+3x+3+2x-5
=3x+4
TRường hợp 3: x>=3
A=2(x-3)+3(x+1)+2x-5
=2x-6+3x+3+2x-5
=7x-8
b: Trường hợp 1: x<-7
B=7-x+2(3-x)-x-4
=3-2x+6-2x=-4x+9
Trường hợp 2: -7<=x<3
B=x+7+2(3-x)-x-4
=3+6-2x=-2x+9
Trường hợp 3: x>=3
B=x+7+2x-6-x-4=2x-3

\(a,A=\dfrac{2x\left(x-3\right)+8\left(x+3\right)-2x-12}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x^2+6}\\ A=\dfrac{2x^2-6x+8x+24-2x-12}{\left(x-3\right)}\cdot\dfrac{1}{x^2+6}\\ A=\dfrac{2x^2+12}{\left(x-3\right)\left(x^2+6\right)}=\dfrac{2\left(x^2+6\right)}{\left(x-3\right)\left(x^2+6\right)}=\dfrac{2}{x-3}\)
\(b,A=5\Leftrightarrow\dfrac{2}{x-3}=5\Leftrightarrow5x-15=2\Leftrightarrow x=\dfrac{17}{5}\)

a. \(A=\left(\dfrac{2-3x}{x^2+2x-3}-\dfrac{x+3}{1-x}-\dfrac{x+1}{x+3}\right):\dfrac{3x+12}{x^3-1}\left(ĐKXĐ:x\ne1;x\ne-3\right)\)
\(=\left(\dfrac{2-3x}{\left(x-1\right)\left(x+3\right)}+\dfrac{x+3}{x-1}-\dfrac{x+1}{x+3}\right):\dfrac{3x+12}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\left(\dfrac{2-3x}{\left(x-1\right)\left(x+3\right)}+\dfrac{\left(x+3\right)^2}{\left(x-1\right)\left(x+3\right)}-\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+3\right)}\right):\dfrac{3x+12}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{2-3x+x^2+6x+9-x^2+1}{\left(x-1\right)\left(x+3\right)}:\dfrac{3x+12}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{3x+12}{\left(x-1\right)\left(x+3\right)}:\dfrac{3x+12}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{3x+12}{\left(x-1\right)\left(x+3\right)}.\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{3x+12}=\dfrac{x^2+x+1}{x+3}\)
\(M=A.B=\dfrac{x^2+x+1}{x+3}.\dfrac{x^2+x-2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+x-2}{x+3}\)
b. -Để M thuộc Z thì:
\(\left(x^2+x-2\right)⋮\left(x+3\right)\)
\(\Rightarrow\left(x^2+3x-2x-6+4\right)⋮\left(x+3\right)\)
\(\Rightarrow\left[x\left(x+3\right)-2\left(x+3\right)+4\right]⋮\left(x+3\right)\)
\(\Rightarrow4⋮\left(x+3\right)\)
\(\Rightarrow x+3\in\left\{1;2;4;-1;-2;-4\right\}\)
\(\Rightarrow x\in\left\{-2;-1;1;-4;-5;-7\right\}\)
c. \(A^{-1}-B=\dfrac{x+3}{x^2+x+1}-\dfrac{x^2+x-2}{x^3-1}\)
\(=\dfrac{x+3}{x^2+x+1}-\dfrac{x^2+x-2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{\left(x+3\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x^2+x-2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2-x+3x-3-x^2-x+2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\)
\(=\dfrac{1}{x^2+2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{3}{4}}=\dfrac{1}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\le\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3}\)
\(Max=\dfrac{4}{3}\Leftrightarrow x=\dfrac{-1}{2}\)


c: \(E=\dfrac{\left(x-5\right)^2}{x\left(x-5\right)}=\dfrac{x-5}{x}\)

Lời giải:
$x=4$ thì $\frac{x}{2}=2=y$
$\Rightarrow y-\frac{x}{2}=0$
Do đó:
$(\frac{x}{2}-y^3)^3-6(y-\frac{x}{2})^2-12(y-\frac{x}{2})-8$
$=(\frac{x}{2}-y^3)^3-8=(2-2^3)^3-8=-224$