Cho hàm số y = f x có đạo hàm f ' x = x 2 x 2 − 4 , x ∈ ℝ . Mệnh đề nào sau đây là đúng ?
A. Hàm số đã cho đạt cực tiểu tại x = − 2.
B. Hàm số đã cho có 3 cực trị.
C. Hàm số đã cho có 2 cực trị.
D. Hàm số đã cho đạt cực đại tại x = 2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có f ' x = x 2 + 3 ≥ 0 ∀ x ∈ R .
Vậy hàm số đồng biến trên .

Đáp án A.
Ta có g ' x = x 2 - 2 ' f ' x 2 - 2 = 2 x . f ' x 2 - 2 ; ∀ x ∈ ℝ .
Khi đó g ' x < 0 ⇔ x . f ' x 2 - 2 < 0 ⇔ [ x < 0 f ' x 2 - 2 > 0 x > 0 f ' x 2 - 2 < 0 ⇔ [ x < 0 x 2 - 2 > 2 x > 0 x 2 - 2 < 2 ⇔ [ 0 < x < 2 x < - 2 .
Vậy hàm số nghịch biến trên khoảng - ∞ ; - 2 và (0;2) khẳng định A là sai.

Ta có ![]()
Suy ra ![]()
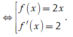
• Từ giả thiết hàm số không có cực trị, kết hợp với đồ thị suy ra hàm số luôn nghịch biến nên f'(x) < 0 với mọi x. Suy ra f'(x) - 2 < 0 với mọi x
• Phương trình f(x) = 2x có nghiệm suy nhất x = 1 (VT nghịch biến – VP đồng biến).
Bảng biến thiên
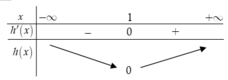
Do đó đồ thị hàm số y = h(x) có điểm cực tiểu M(1;0)
Chọn A.

Đáp án C
Từ giả thiết em có f ' x = − x − 1 2 − 1 < 0 , ∀ x ∈ ℝ . Hàm số f(x) luôn nghịch biến trên − ∞ ; + ∞ .

g’(x)=2f(x).f’(x)-4.f’(x)=2f’(x).[f(x)-2]
Từ đồ thị trên của y=f’(x) suy ra BBT của y=f(x). Suy ra max f(x)=f(1)=1
Do đó f(x)-2< 0, x ϵ R
g’(x)=0→f’(x)=0→x= -1 hoặc x=1.
Lập bảng biến thiên suy ra min g(x)= -3
Đáp án A

Chọn D
Xét hàm số ![]() . Khi đó hàm số
. Khi đó hàm số ![]() liên tục trên các đoạn
liên tục trên các đoạn ![]() ,
, ![]() và có
và có ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() .
.
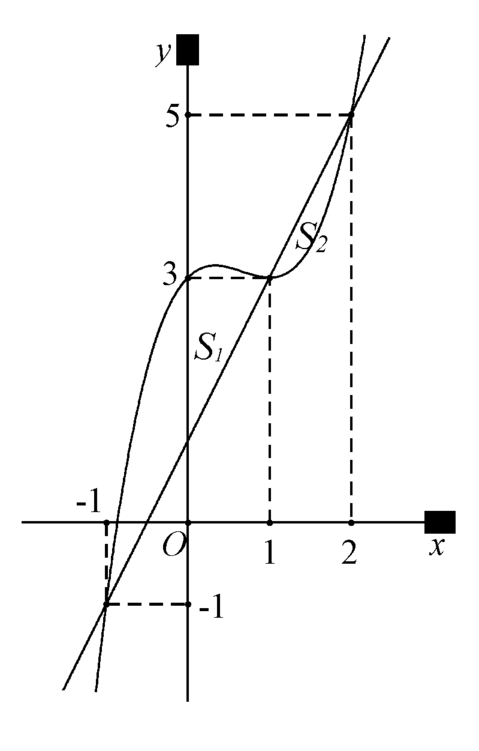
Do đó diện tích hình phẳng giới hạn bởi  là
là
![]()
![]()
![]()
![]() .
.
Vì ![]() nên
nên ![]() .
.
Diện tích hình phẳng giới hạn bởi 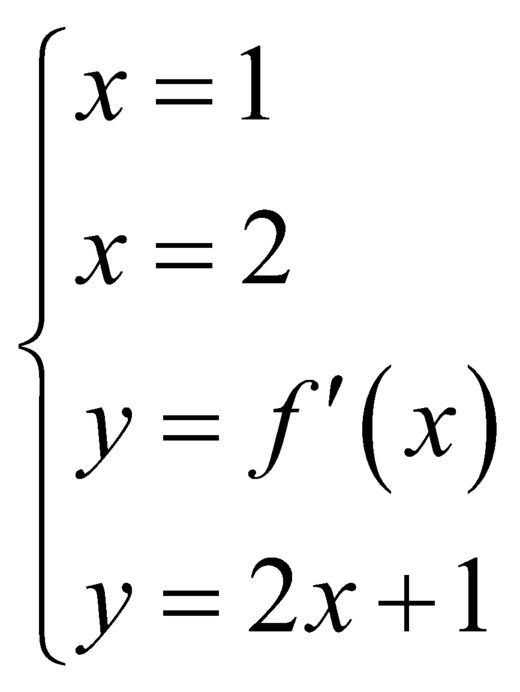 là
là
![]()
![]()
![]()
![]() .
.
Vì ![]() nên
nên ![]() .
.

Ta có:
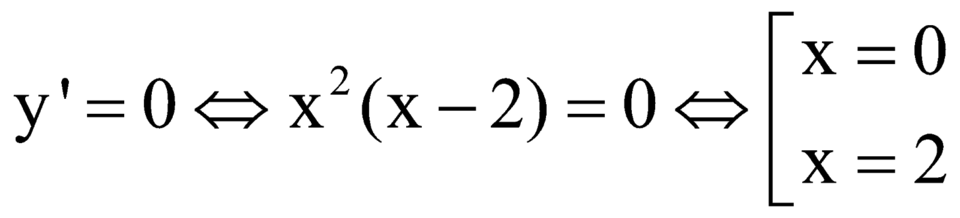
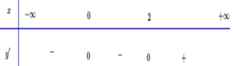
Dựa vào BBT ta thấy hàm số nghịch biến trên ![]() và đồng biến trên
và đồng biến trên ![]()
Chọn D.
Đáp án C.
Ta có bảng xét dấu của y’.
Nhìn vào bảng xét dấu thì hàm số đã cho có 2 cực trị đạt tại x = − 2 ; x = 2 , đạt cực đại tại x = − 2 ; đạt cực tiểu tại x = 2.