Vật có khối lượng m trượt từ điểm cao nhất của một hình cầu bán kính R đang đứng yên trên mặt phẳng nằm ngang. Tới độ cao h nào thì nó rời hình cầu ?. Bỏ qua mọi ma sát, vận tốc ban đầu rất nhỏ.
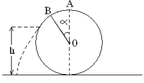
A. h = 3R/2
B. h = 5R/2
C. h = 9R/2
D. h = 7R/2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

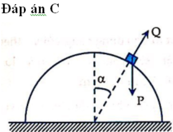
Khi vật trượt trên mặt cầu vật chịu tác dụng của trọng lực P và phản lực Q của mặt cầu có tổng hợp tạo ra gia tốc với hai thành phần tiếp tuyến và hướng tâm. Quá trình chuyển động tuân theo sự bảo toàn cơ năng:
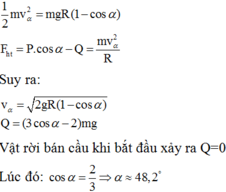

Chọn đáp án C
Tại điểm cao nhất của vòng tròn ta có m v 2 R = N + P ⇒ N = m v 2 R − P ( 1 )
Áp dụng định luật bảo toàn cơ năng cho hai vị trí đó là khi vật ở vị trí có độ cao h và khi vật ở vị trí cao nhất trên vòng tròn m g h = 1 2 m v 2 + m g .2 R ⇒ v 2 = 2 g h − 2 R → 1 N = 2 m g h − 2 R R − m g
Vật không rời tại điểm cao nhất trên vòng tròn khi
N ≥ 0 ⇔ 2 m g h − 2 R R − m g ≥ 0 ⇒ h ≥ 5 R 2 ⇒ h min = 5 R 2
Chú ý: Đối với bài toán hỏi áp lực tại các điểm cao nhất và thấp nhất trên vòng tròn chúng ta chỉ cần tìm độ lớn của phản lực thì suy ra độ lớn áp lực bằng độ lớn phản lực.

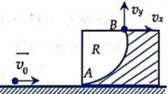
Khi bi tiếp xúc với miếng gỗ, bi đẩy miếng gỗ chuyển động, vận tốc của hòn bi theo phương ngang và vận tốc miếng gỗ theo phương ngang khi tiếp xúc với nhau thì bằng nhau.
Gọi vx là thành phần theo phương ngang của vận tốc hòn bi và vận tốc miếng gỗ khi tiếp xúc.
Áp dụng định luật bảo toàn động lượng cho hệ gồm bi và miếng gỗ phương ngang tại ví trí ban đầu và khi bi đến điểm B, ta được:
![]()
Áp dụng định luật bảo toàn cơ năng cho hệ hòn bi + miếng gỗ tại vị trí ban đầu và khi bi đến điểm B, ta được:
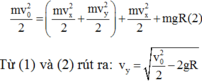
Xét trong hệ qui chiếu đứng yên gắn với mặt đất, sau khi hòn bi tới B nó vạch ra một parabol,
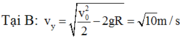
gọi h là chiều cao của đỉnh parabol do hòn bi vạch ra sau khi nó rời khỏi B, ta có
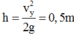
Vậy độ cao tối đa mà hòn bi đạt được là:
H=h+R=62,5cm

a, Khi vật đang ở A, động năng của vật là cực đại và nó bằng thế năng của vật tại B (Wt max):
Wtmax = mgz = 4 . 10 . 0,8 = 32 (J)
⇒ \(\dfrac{1}{2}mv^2=32\)
⇒ v = 4 (m/s)
Vậy khi đến B v = 4 m/s
b, Do có lực ma sát nên cơ năng không được bảo toàn
Độ biến thiên cơ năng bằng công của lực ma sát
Tại B, cơ năng của vật là
W = Wđmax = 32 (J)
Tại C cơ năng của vật là
W = Wt + Wđ = 40. BC
Ta có 40BC - 32 = F . BC
⇒ 40BC - 32 = N . 0.25 . BC
⇒ 40BC - 32 = 10BC
⇒ BC = \(\dfrac{32}{30}=1,06\left(m\right)\)

Đáp án A
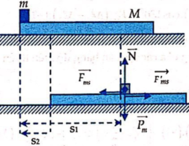
+ Ngoại lực tác dụng lên hệ 2 vật chỉ có phương thẳng đứng => Động lượng hệ bảo toàn theo phương ngang.
+ Khi m dừng lại trên M thì 2 vật chuyển động với cùng vận tốc v.
+ Áp dụng ĐLBTĐL cho thời điểm ban đầu và khi m dừng lại trên M:
![]()
+ Theo phương ngang m và M chịu của![]()
+ s1, s2 là quãng đường m và M chuyển động được tới khi m dừng lại trên M, quãng đường m trượt được trên M là s=s1- s2
+ Áp dụng định lý động năng:
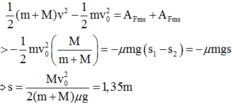

Đáp án A
Vận tốc của hệ hai vật sau khi va chạm
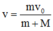
= 0,4 m/s
Quá trình va chạm không làm thay đổi vị trí cân bằng của hệ
→ v = v m a x
→ Biên độ dao động mới
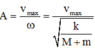
= 5cm