Cho hình chóp S.ABCD có S A ⊥ ( A B C D ) , ABCD là hình chữ nhật có AB =a, AD =2a, S A = a 3 . Tính tan của góc giữa hai mặt phẳng (SBD) và (ABCD).
A. 2 5 5
B. 3 5 2
C. 15 3
D. 15 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

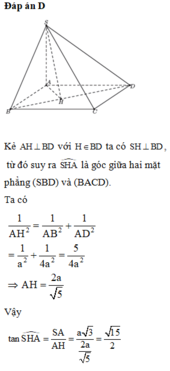

Đáp án D
Kẻ A H ⊥ B D với H ∈ B D ta có S H ⊥ B D , từ đó suy ra S H A ^ là góc giữa hai mặt phẳng (SBD) và (BACD).
Ta có 1 A H 2 = 1 A B 2 + 1 A D 2 = 1 a 2 + 1 4 a 2 = 5 4 a 2 ⇒ A H = 2 a 5
Vậy tan S H A ^ = S A A H = a 3 2 a 5 = 15 2
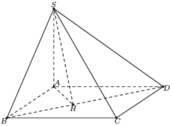

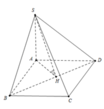
Đáp án C
Dựng A H ⊥ B D , lại có
S A ⊥ S H A ⇒ S B D ; A B C D ^ = S H A ^
Ta có A H = 2 a 5 ⇒ tan α = S A A H = 15 2

Đáp án C
Kẻ AH ⊥BD
Khi đó ![]()
![]()
Mà ![]() nên góc giữa (SBD) và (ABCD) là SHA=α.
nên góc giữa (SBD) và (ABCD) là SHA=α.
Suy ra 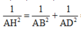
![]()
![]()
Do đó ![]()