Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng 2a. Cosin của góc tạo bởi cạnh bên và mặt phẳng đáy bằng:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


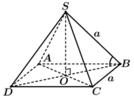
Xác định được góc cần tìm là
![]()
Trong tam giác vuông ta có
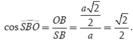
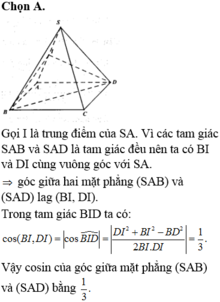
Chọn A.

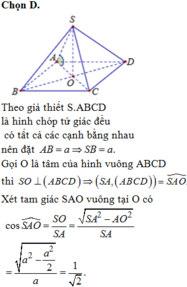
Chọn D.
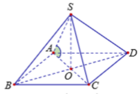
Theo giả thiết S.ABCD là hình chóp tứ giác đều có tất cả các cạnh bằng nhau nên đặt AB = a => SB = a.
Gọi O là tâm của hình vuông ABCD thì ![]()
Xét tam giác SAO vuông tại O có 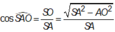
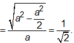

tham khảo
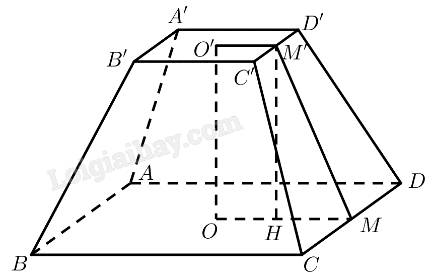
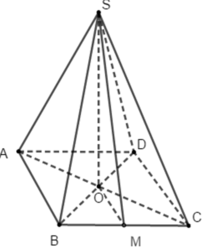
Mô hình hoá chân cột bằng gang bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy.Vậy \(AB=2a,A'B'=a,OO'=2a\)
a)Gọi \(M,M'\) lần lượt là trung điểm của \(CD,C'D'.\)
\(A'B'C'D'\) là hình vuông \(\Rightarrow O'M\perp C'D\)
\(CDD'C\) là hình thang cân \(\Rightarrow MM'\perp C'D'\)
Vậy \(\widehat{MM'O}\) là góc phẳng nhị diện giữa mặt bên và đáy nhỏ,\(\widehat{M'MO}\) là góc phẳng nhị diện giữa mặt bên và đáy lớn.
Kẻ \(M'H\perp OM\left(H\in OM\right)\)
\(OMM'O'\) là hình chữ nhật
\(\Rightarrow OH=O'M'=\dfrac{a}{2},OM=a,MH=OM-OH=\dfrac{a}{2}\tan\widehat{M'MO}=\dfrac{M'H}{MH}=4\)
\(\Rightarrow\widehat{M'MO}=75,96^o\Rightarrow\widehat{MM'O'}=180^o-\widehat{M'MO}\\ =104,04^o\)
b)Diện tích đáy lớn là:\(S=AB^2=4a^{^2}\)
Diện tích đáy bé là:\(S'=A'B'^2=a^2\)
Thể tích hình chóp cụt là:
\(V_1=\dfrac{1}{3}h\left(S+\sqrt{SS'}+S'\right)\\ =\dfrac{1}{3}.2a\left(4a^2+\sqrt{4a^2.a^2}+a^2\right)=\dfrac{14a^3}{3}\)
Thể tích hình trụ rỗng là:\(V_2=\pi R^2h=\pi\left(\dfrac{a}{2}\right)^2.2a=\dfrac{\pi a^3}{2}\)
Thể tích chân cột là:\(V=V_1-V_2=\left(\dfrac{14}{3}-\dfrac{\pi}{2}\right)a^3\)

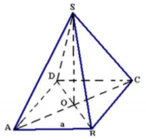
Gọi O là tâm của hình vuông ABCD. Do S.ABCD là hình chóp tứ giác đều
nên S O ⊥ A B C D
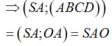
ABCD là hình vuông cạnh
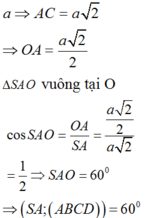
Chọn D.

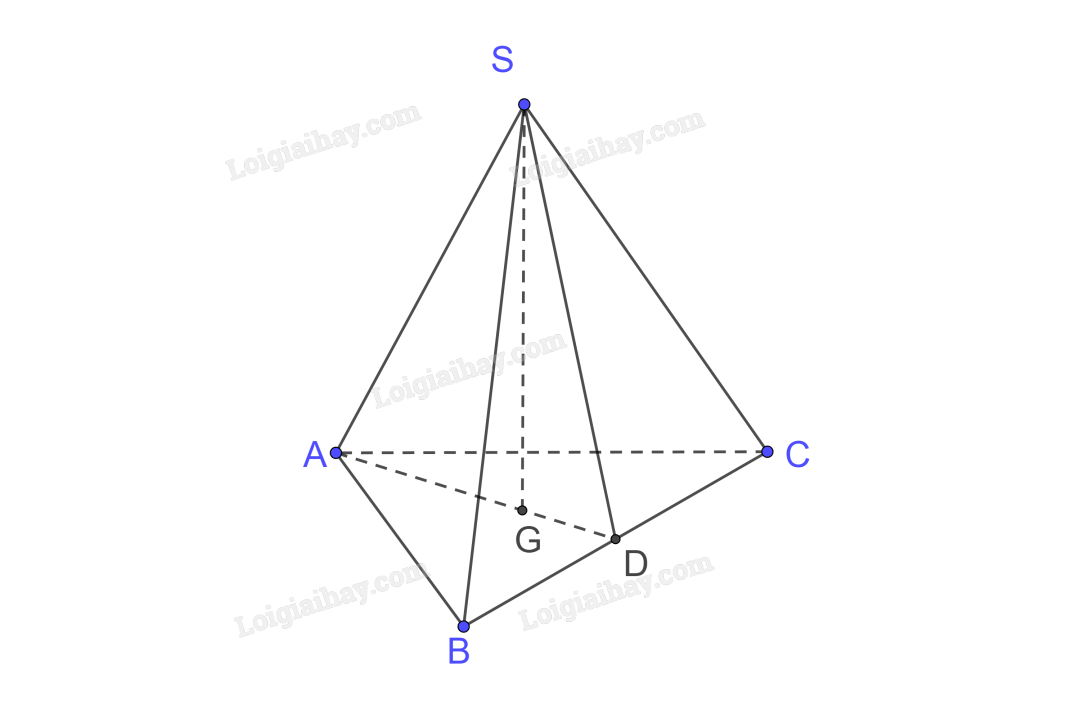
Vì hình chóp S.ABC đều, gọi G là hình chiếu của S trên (ABC) nên G là tâm của đáy ABC là tam giác đều do đó G cũng là trọng tâm hay trực tâm của tam giác ABC.
Gọi AG cắt BC tại D
a) Ta có A là hình chiếu của A trên (ABC)
G là hình chiếu của S trên (ABC)
\( \Rightarrow \) AG là hình chiếu của SA trên (ABC)
\( \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \left( {SA,AG} \right) = \widehat {SAG}\)
Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)
Mà G là trọng tâm nên \(AG = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)
Xét tam giác SAG vuông tại G có
\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \)
\(\sin \widehat {SAG} = \frac{{SG}}{{SA}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :b = \sqrt {1 - \frac{{{a^2}}}{{3{b^2}}}} \)
b) Ta có \(AG \bot BC,SG \bot BC \Rightarrow BC \bot \left( {SAD} \right);SD \subset \left( {SAD} \right) \Rightarrow BC \bot SD\)
\(BC \bot AD\) (G là trực tâm)
\(\begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\ \Rightarrow \left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \left( {AD,SD} \right) = \widehat {SDA}\end{array}\)
Mà G là trọng tâm nên \(GD = \frac{1}{3}AD = \frac{{a\sqrt 3 }}{6}\)
Xét tam giác SGD vuông tại G có
\(\tan \widehat {SGD} = \frac{{SG}}{{GD}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :\frac{{a\sqrt 3 }}{6} = \frac{6}{{a\sqrt 3 }}.\sqrt {{b^2} - \frac{{{a^2}}}{3}} \)

Chân đường cao hình chóp đều S.ABCD trùng với tâm O của đáy ABCD. AO là hình chiếu của SA lên (ABCD)
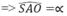
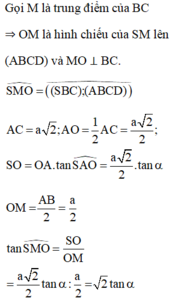
Đáp án C

Gọi O là giao điểm của AC và BD.
Vì S, ABCD là hình chóp tứ giác đều nên
Hình chiếu vuông góc của điểm S lên mp(ABCD) là điểm O nên góc giữa cạnh bên và mặt phẳng đáy là góc SBO.
Ta có: B D = a 2 ; B O = 1 2 B D = a 2
Lại có: S B 2 + S D 2 = B D 2 = 2 a 2 nên tam giác SBD vuông cân tại S. ⇒ S B O ^ = 45 0
Đáp án C
Chọn D
Phương pháp
Góc giữa cạnh bên SA với mặt đáy là góc giữa SA và hình chiếu của SA trên mặt phẳng đáy.
Gọi O là giao điểm của AC và BD
Ta có SABCD là hình chóp đều nên O là hình chiếu của S trên
(ABCD).