Cho tứ diện OABC có OA, OB, OC, OD đôi một vuông góc nhau, biết rằng OA = 2OB=3OC =3a. Tính khoảng cách d từ O đến mặt phẳng (ABC).
A. d = 2 a 14
B. d = 3 a 13
C. d = 3 a 11
D. d = 3 a 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi I là hình chiếu của O trên BC, H là hình chiếu của O trên AI.
Suy ra d = OH.
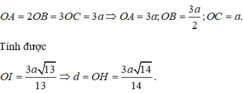

Đáp án D
Gọi H là hình chiếu của O xuống (ABC)
Ta có: 1 O H 2 = 1 a 2 + 1 2 a 2 + 1 a 3 2 = 19 12 a 2 ⇒ O H = 2 a 3 19

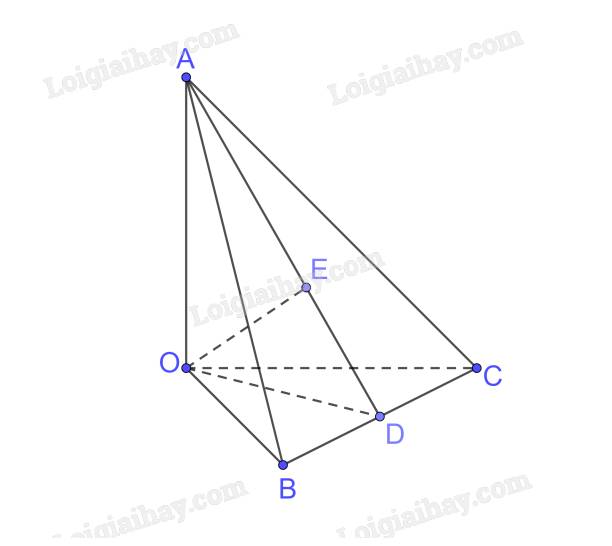
Ta có \(OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {OBC} \right);BC \subset \left( {OBC} \right) \Rightarrow OA \bot BC\)
Trong (OBC) kẻ \(OD \bot BC\)
\(\begin{array}{l} \Rightarrow BC \bot \left( {OAD} \right);BC \subset \left( {ABC} \right) \Rightarrow \left( {OAD} \right) \bot \left( {ABC} \right)\\\left( {OAD} \right) \cap \left( {ABC} \right) = AD\end{array}\)
Trong (OAD) kẻ \(OE \bot AD\)
\( \Rightarrow OE \bot \left( {ABC} \right) \Rightarrow d\left( {O,\left( {ABC} \right)} \right) = OE\)
Xét tam giác OBC vuông tại O có
\(\frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {2a} \right)}^2}}} = \frac{3}{{4{a^2}}} \Rightarrow OD = \frac{{2a\sqrt 3 }}{3}\)
Xét tam giác OAD vuông tại O có
\(\frac{1}{{O{E^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{D^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{2a\sqrt 3 }}{3}} \right)}^2}}} = \frac{7}{{4{a^2}}} \Rightarrow OE = \frac{{2a\sqrt 7 }}{7}\)
Vậy \(d\left( {O,\left( {ABC} \right)} \right) = \frac{{2a\sqrt 7 }}{7}\)

Đáp án A
Gọi H là hình chiếu của O lên mặt phẳng (ABC) nên O H ⊥ A B C ⇒ O H ⊥ B C 1 .
Mặt khác O A ⊥ O B , O A ⊥ O C ⇒ O A ⊥ O B C ⇒ O A ⊥ B C 2 .
Từ (1),(2) suy ra B C ⊥ A O H ⇒ B C ⊥ A H . Chứng minh tương tự ta được A B ⊥ C H . Suy ra H là trực tâm của ΔABC.
Trong mặt phẳng (ABC) gọi E là giao điểm của AH và BC.
Ta có O H ⊥ A B C ⇒ O H ⊥ A E tại H.
O A ⊥ A B C ⇒ O A ⊥ O E tức là OH là đường cao của tam giác vuông OAE.
Mặt khác OE là đường cao của tam giác vuông OBC.
Do đó: 1 O H 2 = 1 O A 2 + 1 O E 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 .
⇔ 1 d 2 = 1 a 2 + 1 b 2 + 1 c 2 ⇒ d = a b c b 2 c 2 + a 2 c 2 + a 2 b 2 .

Đáp án D
Ta có: V O . A B C = 1 6 O A . O B . O C = 6 ⇒ O C = 3
Lại có 1 d O ; A B C 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 ⇒ d O ; A B C = 12 41

Bạn tự vẽ hình nhé!
Giả sử: OC = a ⇒ OB = 3/2a và OA = 3a
Xét tam giác OAB vuông tại O có: \(AB=\sqrt{OA^2+OB^2}=\dfrac{3\sqrt{5}}{2}a\)
\(\Rightarrow AM=BM=OM=\dfrac{1}{2}AB=\dfrac{3\sqrt{5}}{4}a\)
Xét tam giác OMA, có:
\(\cos\widehat{AOM}=\dfrac{OM^2+OA^2-AM^2}{2OM.OA}=\dfrac{OA}{2OM}=\dfrac{2\sqrt{5}}{5}\)
Xét tam giác OMB, có:
\(\cos\widehat{BOM}=\dfrac{OM^2+OB^2-BM^2}{2OM.OB}=\dfrac{OB}{2OM}=\dfrac{\sqrt{5}}{4}\)
Ta có: \(\overrightarrow{OM}.\overrightarrow{AB}=\overrightarrow{OM}\left(\overrightarrow{OB}-\overrightarrow{OA}\right)=\overrightarrow{OM}.\overrightarrow{OB}-\overrightarrow{OM}.\overrightarrow{OA}\)
\(=\dfrac{3\sqrt{5}}{4}a.\dfrac{3}{2}a.\dfrac{2\sqrt{5}}{5}-\dfrac{3\sqrt{5}}{4}a.3a.\dfrac{\sqrt{5}}{4}=\dfrac{-9}{16}a^2\)
\(\Rightarrow\cos\widehat{\left(\overrightarrow{OM},\overrightarrow{AB}\right)=\dfrac{\overrightarrow{OM}.\overrightarrow{AB}}{OM.AB}=-\dfrac{1}{10}}\)
\(\Rightarrow cos\left(OM,AB\right)=\dfrac{1}{10}\)
Hicc, ở phần tính cos BOM mình bấm máy nhầm, bạn tự bấm lại nhé. :((((
Còn cả đoạn thay cos AOM và cos BOM vào tích vô hướng cũng bị lộn giữa 2 góc á.
Kết quả ra là 3/5 nhé!
Tự dưng giờ xem lại mới nhận ra lỗi sai nghiêm trọng này. Xin lỗi bạn nhé!
Đáp án A
Gọi I là hình chiếu của O trên BC, H là hình chiếu của O trên AI.
Suy ra d = OH
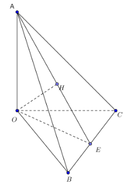
OA = 2OB=3OC =3a
Tính được