Cho hình chóp tam giác đều SABC có chiều cao 2a cạnh bên bằng a. Tính thể tích V của khối chóp SABC. ...
Đọc tiếp
Cho hình chóp tam giác đều SABC có chiều cao 2a cạnh bên bằng a. Tính thể tích V của khối chóp SABC.
K
Khách
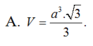
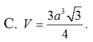
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 1 2017
Chọn C
Phương pháp:
Cách giải:
Hình chóp tam giác đều ABC có chiều cao a, cạnh bên 2a.
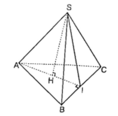
Gọi H là trọng tâm tam giác ABC => SH là đường cao hình chóp => SH = a
Gọi I là trung điểm BC
Do tam giác ABC đều
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 8 2021
Gọi H là hình chiếu vuông góc của S lên đáy \(\Rightarrow\) H là tâm đường tròn ngoại tiếp tam giác ABC
Gọi M là trung điểm BC, do tam giác cân tại A \(\Rightarrow H\in AM\)
Kéo dài AM cắt đường tròn ngoại tiếp tam giác tại D \(\Rightarrow\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\Delta ABD\) vuông tại B
\(BM=\dfrac{1}{2}BC=\dfrac{3a}{2}\) \(\Rightarrow AM=\sqrt{AB^2-BM^2}=\dfrac{a\sqrt{7}}{2}\)
Áp dụng hệ thức lượng:
\(AB^2=AM.AD\Rightarrow AD=\dfrac{AB^2}{AM}=\dfrac{8a\sqrt{7}}{7}\)
\(\Rightarrow AH=\dfrac{AD}{2}=\dfrac{4a\sqrt{7}}{7}\)
\(\Rightarrow SH=\sqrt{SA^2-AH^2}=\dfrac{2a\sqrt{21}}{7}\)
\(V=\dfrac{1}{3}SH.\dfrac{1}{2}AM.BC=...\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 8 2021
Gọi H là hình chiếu vuông góc của S lên đáy
\(\Rightarrow\widehat{SAH}=\widehat{SBH}=\widehat{SCH}=60^0\)
\(\Rightarrow AH=BH=CH=\dfrac{SH}{tan60^0}\Rightarrow H\) là tâm đường tròn ngoại tiếp tam giác đáy
\(\Rightarrow AH=R=\dfrac{AB.BC.AC}{4S_{ABC}}\)
\(\Rightarrow SH=AH.tan60^0=\dfrac{AB.BC.AC.\sqrt{3}}{4S_{ABC}}\)
\(V=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{AB.BC.CA.\sqrt{3}}{4S_{ABC}}.S_{ABC}=\dfrac{5a^3\sqrt{3}}{12}\)
Đáp án C