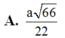
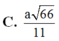
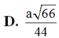
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
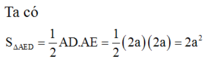
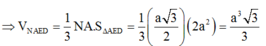
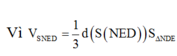
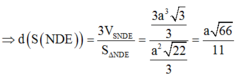
Đáp án B
Gọi K = C D ∩ A B khi đó BC là đường trung bình trong tam giác KAD nên KB =a
Gọi I = K N ∩ A M
Ta có
I M I A = M N K B = 1 2 ⇒ d M = 1 2 d A
Do C E = 1 2 A D nên Δ A C D vuông tại C
Dựng A H ⊥ N C ,
d A = A H = N A . A C N A 2 + A C 2 = a 66 11
Do đó d M = a 66 22
Chọn B.
Phương pháp:
Gắn hệ trục tọa độ.
Cách giải:
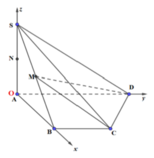
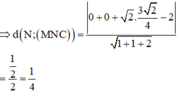
Vây, khoảng cách từ N đến mặt phẳng (MCD) bằng: 1 4 a
Đáp án C
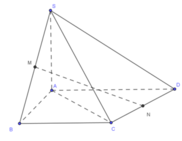
Kẻ CN
⊥
AB ta dễ dàng tính được 
=> tam giác ADC vuông tại C. Từ đó NC ⊥ (SAC)
Gọi O là trung điểm của AC, dễ dàng cm được BD ⊥ (SAC)
=> MK ⊥ (SAC). vơí K là trung điểm của SO, từ đó KC là hc của MN lên .
Ta kẻ KZ ⊥ AC
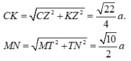
với T là trung điểm của AB.
Gọi α là góc tạo với MN và (SAC)
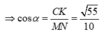
Chọn C
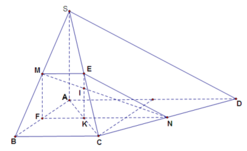
Ta gọi E, F lần lượt là trung điểm của SC, AB
Ta có ME//NF(do cùng song song với BC. Nên tứ giác MENF là hình thang, và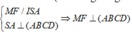 
hay tứ giác MENF là hình thang vuông tại M, F
Ta có: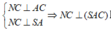 
hay E là hình chiếu vuông góc của N lên (SAC)
Từ đó ta có được, góc giữa MN và (SAC) là góc giữa MN và CI
Suy ra, gọi
α
là góc giữa MN và (SAC) thì 
