cho đường thẳng (d) -x/3 + y/2 =1
a) xác định hệ số góc ,tung độ gốc của (d)
b) tính góc tạo bởi (d) và trục Ox
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 12 2021
\(a,\Leftrightarrow3m-1=-2\Leftrightarrow m=-\dfrac{1}{3}\Leftrightarrow\left(d\right):y=-\dfrac{1}{3}x-1\\ c,\text{Hs góc: }-\dfrac{1}{3}\\ \text{Gọi góc cần tìm là }\alpha>90^0\\ \Leftrightarrow\tan\left(180^0-\alpha\right)=\dfrac{1}{3}\approx\tan18^0\\ \Leftrightarrow\alpha\approx180^0-18^0=162^0\)
12 tháng 1 2022
a: Thay x=1 và y=-2 vào y=ax+1, ta được:
a+1=-2
hay a=-3
Vậy: (d'): y=-3x+1
c: Tọa độ giao điểm của (d) và (d') là:
\(\left\{{}\begin{matrix}-3x+1=x+3\\y=x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=3-\dfrac{1}{2}=\dfrac{5}{2}\end{matrix}\right.\)
19 tháng 12 2021
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x-1=-x+3\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
17 tháng 9 2021
Đề không rõ ràng. Bạn coi lại đề. Những dữ kiện trên được chia theo phần hay là cả 1 cụm?
8 tháng 12 2023
a: Vì (d)//y=1/2x+1 nên \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b\ne1\end{matrix}\right.\)
Vậy: (d): \(y=\dfrac{1}{2}x+b\)
Thay x=2 và y=2 vào (d), ta được:
\(b+\dfrac{1}{2}\cdot2=2\)
=>b+1=2
=>b=1
vậy: (d): \(y=\dfrac{1}{2}x+1\)
b: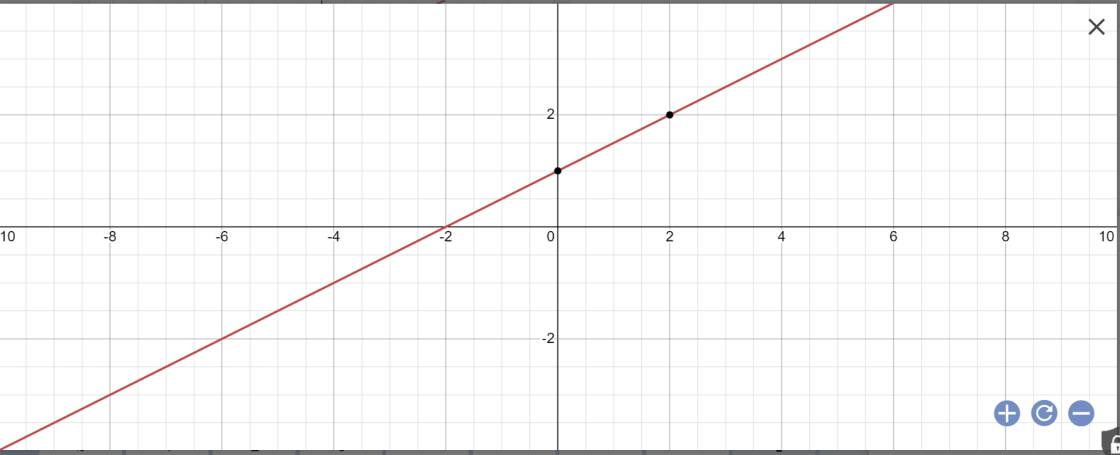 
c: Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
Ta có: (d): \(y=\dfrac{1}{2}x+1\)
=>a=1/2
=>\(tan\alpha=a=\dfrac{1}{2}\)
=>\(\alpha\simeq26^034'\)
d: tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x+1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-2\end{matrix}\right.\)
Tọa độ C là;
\(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}x+1=\dfrac{1}{2}\cdot0+1=1\end{matrix}\right.\)
Vậy: B(-2;0); C(1;0)
\(OB=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{2^2+0^2}=2\)
\(OC=\sqrt{\left(1-0\right)^2+\left(0-0\right)^2}=\sqrt{1^2+0^2}=1\)
Vì Ox\(\perp\)Oy nên OB\(\perp\)OC
=>ΔBOC vuông tại O
=>\(S_{BOC}=\dfrac{1}{2}\cdot OB\cdot OC=\dfrac{1}{2}\cdot2\cdot1=1\)
a: (d): \(-\dfrac{1}{3}x+\dfrac{1}{2}y=1\)
\(\Leftrightarrow y\cdot\dfrac{1}{2}=1+\dfrac{1}{3}x\)
\(\Leftrightarrow y=2+\dfrac{2}{3}x\)
Hệ số góc là 2/3
Tung độ gốc là 2