Cho hai mặt cầu ( S 1 ) v à ( S 2 ) đồng tâm I, có bán kính lần lượt là R 1 = 2 v à R 2 = 10 . Xét tứ diện ABCD có hai đỉnh A , B nằm trên ( S 1 ) và hai đỉnh C , D nằm trên ( S 2 ) . Thể tích lớn nhất của khối tứ diện ABCD bằng
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Từ phương trình mặt cầu (S): ( x - 1 ) 2 + ( y + 2 ) 2 + z 2 = 9 suy ra mặt cầu (S) có tâm I(1;-2;0) và bán kính R=3.

Đáp án C
Ta có: II' = 6 = R + R'
Ta có: MN ≥ MI + II' + I'N = R + 6 + R' = 12
Dấu bằng xảy ra khi M, I, I', N theo thứ tự nằm trên một đường thẳng. Do đó M là giao điểm của tia đối của tia II' với mặt cầu (S), N là giao điểm của tia đối của tia I’I với mặt cầu (S’). Vậy đáp án đúng là C.

Đáp án D.
Mặt cầu tiếp xúc với cả ba mặt cầu trên là mặt cầu tiếp xúc ngoài với cả 3 mặt cầu trên. Gọi I là tâm và R là bán kính mặt cầu cần tìm
Ta có:
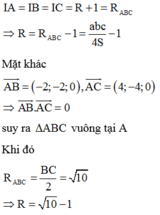

Chọn đáp án D
Giả sử mặt cầu (S) có tâm I m ; 0 ; 0 và bán kính là R (do I ∈ O x ).
Ta có
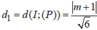
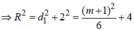
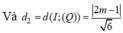
![]()
Từ đó suy ra
![]()
![]()
Để có đúng một mặt cầu (S) thỏa mãn yêu cầu khi và chỉ khi phương trình (*) có đúng một nghiệm m, tức là
![]()
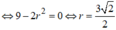
Đáp án đúng : D