Với hai số phức z 1 và z 2 thỏa mãn z 1 z 2 = 8 6 i và z 1...

PT

Pham Trong Bach

13 tháng 9 2018

Với hai số phức z 1 và z 2 thỏa mãn z 1 + z 2 = 8 + 6 i và z 1 - z 2 = 2 tìm giá trị lớn nhất P = z 1 + z 2 ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

13 tháng 9 2018

Đáp án B

Đúng(0)

A

AllesKlar

23 tháng 4 2022

Tìm tất cả các số phức \(z\) thỏa mãn điều kiện:

\(\left|iz-1-3i\right|.\left|\overline{z}+1+i\right|=\left|z^2+\left(-6+2i\right)z+8-6i\right|\) và \(\dfrac{z-3}{z+2}\) là số thuần ảo.

#Toán lớp 12

0

PT

Pham Trong Bach

31 tháng 12 2018

Phần thực và phần ảo của số phức z thỏa mãn: (1 + i)²(2 - i) z = 8 + i + (1 + 2i)z lần lượt là?

A. -3; -2

B. 2; 3

C. 2; -3

D. Đáp án khác.

#Toán lớp 12

1

CM

Cao Minh Tâm

31 tháng 12 2018

Chọn C.

Ta có: ( 1 + i)²(2 - i) z = 8 + i + (1 + 2i)z

Nên z[( 1 + i)²(2 -i) – (1 + 2i) ] = 8 + i

Suy ra: z[2i(2 - i) – 1 - 2i] = 8 + i

Vậy số phức z đã cho có phần thực là 2, phần ảo là -3.

Đúng(0)

PT

Pham Trong Bach

12 tháng 4 2018

Có bao nhiêu giá trị nguyên của m để có đúng 2 số phức z thỏa mãn z - ( m - 1 ) + i = 8 và z - 1 + i = z - 2 + 3 i .

A. 130

B. 66

C. 65

D. 131

#Toán lớp 12

1

CM

Cao Minh Tâm

12 tháng 4 2018

Đúng(0)

PT

Pham Trong Bach

23 tháng 4 2019

Tìm số phức z thỏa mãn |z-2|=|z| và (z+1)( z ¯ - i ) là số thực

A. z = 1 + 2 i

B. z = - 1 - 2 i

C. z = 2 - i

D. z = 1 - 2 i

#Mẫu giáo

1

CM

Cao Minh Tâm

23 tháng 4 2019

Đúng(0)

PT

Pham Trong Bach

30 tháng 1 2017

Tìm số phức z thỏa mãn |z-2| = |z| và |z+1|( z ¯ -i) là số thực.

A. z = 1 - 2i

B. z = -1 - 2i

C. z = 2 - i

D. z = 1 + 2i

#Toán lớp 12

1

CM

Cao Minh Tâm

30 tháng 1 2017

Đáp án A

Đặt z = a + bi;

Mặt khác là số thực, suy ra

Đúng(0)

PT

Pham Trong Bach

4 tháng 2 2018

Tìm số phức z thỏa mãn z - 2 = z và ( z + 1 ) ( z ¯ - i ) là số thực

A. z=1+2i

B. z=-1-2i

C. z=2-i

D. z=1-2i

#Toán lớp 12

1

CM

Cao Minh Tâm

4 tháng 2 2018

Đáp án D

Phương pháp.

Gọi . Sử dụng giả thiết để tìm a, bsuy ra giá trị của z.

Lời giải chi tiết.

Giả sử .Khi đó ta có

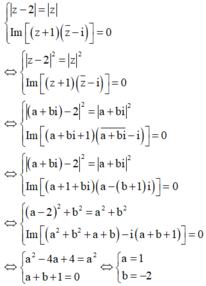
Vậy z=a+bi=1-2i

Sai lầm.Một số học sinh có thể nhớ nhầm i 2 = - 1 thành i 2 = 1 do đó quá trình tính toán kết quả sẽ bị sai.

Đúng(0)

PT

Pham Trong Bach

19 tháng 3 2017

Tìm số phức z thỏa mãn |z-2| = |z| và (z+1)( z ¯ -i) là số thực.

A. z = 1 - 2i

B. z = -1 - 2i

C. z = 2 - i

D. z = 1 + 2i

#Toán lớp 12

1

CM

Cao Minh Tâm

19 tháng 3 2017

Đáp án A

Đặt

Mặt khác là số thực, suy ra

b+2 = 0

Đúng(0)

PT

Pham Trong Bach

7 tháng 3 2019

Tìm phần thực a của số phức z thỏa mãn (1 + i) 2( 2 - i) z = 8 + i + (1 + 2i) z. A. a = 2. B. a = -3. C. a = -2. D. a =...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

7 tháng 3 2019

Chọn A.

Ta có: (1 + i) ²( 2 - i) z = 8 + i + (1 + 2i) z.

Suy ra: (2 + 4i)z - (1 + 2i)z = 8 = i

Vậy phần thực của z bằng 2.

Đúng(0)

PT

Pham Trong Bach

13 tháng 3 2017

Cho số phức z thỏa mãn 1 + i z là số thực và |z-2|=m với m ∈ R. Gọi m 0 là một giá trị của m để có đúng một số phức thỏa mãn bài toán. Khi đó A. m 0 ∈ ( 0 ; 1 / 2 ) B. m 0 ∈ ( 1 / 2 ; 1 ) C. m 0 ∈ ( 3 / 2 ; 2 ) D. m 0 ∈ ( 1 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

13 tháng 3 2017

Đúng(0)

PT

Pham Trong Bach

7 tháng 4 2017

Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b

A. P = -1

B. P = -5

C. P = 3

D. P = 7

#Toán lớp 12

1

CM

Cao Minh Tâm

7 tháng 4 2017

Đáp án D.

Đặt z = a + bi => a + bi

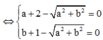
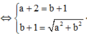
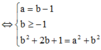
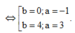
Do |z| > 1 => a = 3, b = 4

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP