Cho hàm số f(x), f(-x) liên tục trên ℝ và thỏa mãn 2f(x)+3f(-x)= 1 4 + x 2 . Tính I = ∫ - 2 2 f ( x ) d x .
![]()
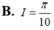
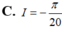
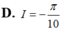
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Lấy tích phân hai vế của biểu thức 2 f ( x ) + 3 f - x = 1 4 + x 2 , ta được
2 ∫ - 2 2 f ( x ) d x + 3 ∫ - 2 2 f ( - x ) d x = ∫ - 2 2 1 4 + x 2 d x ⇔ 2 I + 3 ∫ - 2 2 f ( - x ) d x = π 4
Xét J = ∫ - 2 2 f ( - x ) d x . Đặt t = - x ⇒ d t = - d x . Đổi cận: x = - 2 → t = 2 x = 2 → t = - 2
Suy ra J = - ∫ 2 - 2 f ( t ) d t = ∫ - 2 2 f ( t ) d t = ∫ - 2 2 f ( x ) d x = I .
Vậy 2 I + 3 ∫ - 2 2 f ( x ) d x = π 4 ⇔ 2 I + 3 I = π 4 ⇔ I = π 20 .

Đáp án C.
Ta có f 2 - f 1 = ∫ 1 2 f ' x d x ≥ ∫ 1 2 x + 1 x d x = x 2 2 + ln x 1 2 = 2 + ln 2 - 1 2 = 3 2 + ln 2 .
Mặt khác f 1 = 1 suy ra f 2 ≥ f 1 + 3 2 + ln 2 = 1 + 3 2 + ln 2 = 5 2 + ln 2 .
Chọn A