Tổng số đo các góc ngoài của một tam giác bằng
(mỗi đỉnh tính 1 góc ngoài)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. B = 55 độ
C = 35
b. lỗi. phải là 360 độ
ông họ ngô
tôi họ đinh

Lời giải:
Gọi $\widehat{A}, \widehat{B}, \widehat{C}$ là 3 góc trong tam giác $ABC$ và $\widehat{A_1}, \widehat{B_1}, \widehat{C_1}$ tương ứng là 3 góc ngoài 3 đỉnh.
Ta có:
$\widehat{A_1}+\widehat{B_1}+\widehat{C_1}=(180^0-\widehat{A})+(180^0-\widehat{B})+(180^0-\widehat{C})$
$=540^0-(\widehat{A}+\widehat{B}+\widehat{C})$
$=540^0-180^0=360^0$

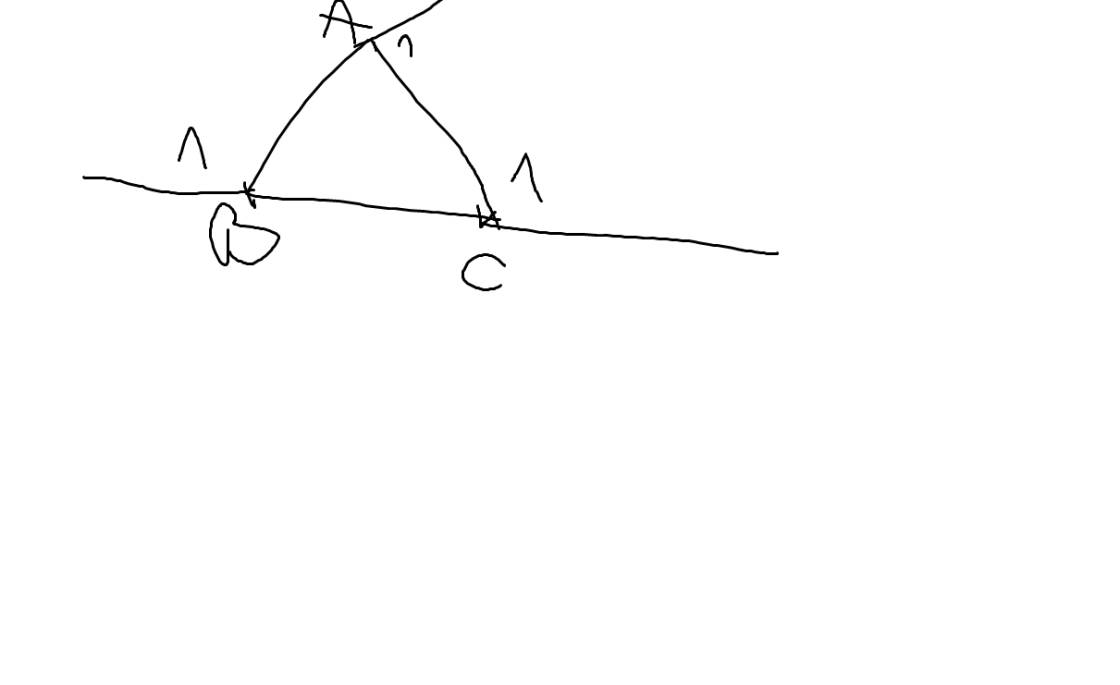
Gọi \(\widehat{A_1};\widehat{B_1};\widehat{C_1}\) lần lượt là các góc ngoài tại các đỉnh A,B,C của ΔABC
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\widehat{B_1}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{B_1}=180^0-\widehat{ABC}\)
\(\widehat{C_1}+\widehat{ACB}=180^0\)(hai góc kề bù)
=>\(\widehat{C_1}=180^0-\widehat{ACB}\)
\(\widehat{A_1}+\widehat{BAC}=180^0\)(hai góc kề bù)
=>\(\widehat{A_1}=180^0-\widehat{BAC}\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}\)
\(=180^0-\widehat{BAC}+180^0-\widehat{ABC}+180^0-\widehat{ACB}\)
\(=540^0-180^0=360^0\)

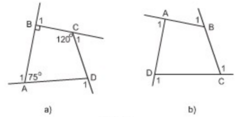
a) + Góc ngoài tại A là góc A1:
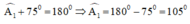
+ Góc ngoài tại B là góc B1:
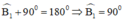
+ Góc ngoài tại C là góc C1:

+ Góc ngoài tại D là góc D1:
Theo định lý tổng các góc trong một tứ giác bằng 360º ta có:
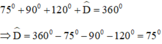
Lại có:
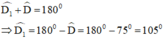
Vậy góc ngoài tại D bằng 105º.
b) Hình 7b:
Ta có:
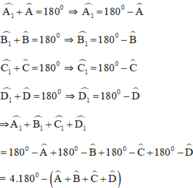
Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có:
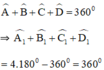
c) Nhận xét: Tổng các góc ngoài của tứ giác cũng bằng 360º.

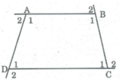
Ta có: ∠ A 1 + ∠ B 1 + ∠ C 1 + ∠ D 1 = 360 o (tổng các góc của tứ giác)
+) Lại có: ∠ A 1 + ∠ A 2 = 180 o ( hai góc kề bù).
∠ B 1 + ∠ B 2 = 180 o (hai góc kề bù)
∠ C 1 + ∠ C 2 = 180 o (hai góc kề bù)
∠ D 1 + ∠ D 2 = 180 o (hai góc kề bù)
Suy ra: ∠ A 1 + ∠ A 2 + ∠ B 1 + ∠ B 2 + ∠ C 1 + ∠ C 2 + ∠ D 1 + ∠ D 2 = 180 0 . 4 = 720 0
⇒ ∠ A 2 + ∠ B 2 + ∠ C 2 + ∠ D 2 = 720 0 - ∠ A 1 + ∠ B 1 + ∠ C 1 + ∠ D 1
= 720 0 - 360 0 = 360 0

Bài 1:
Số đo góc ngoài tại đỉnh C là \(74^0+47^0=121^0\)
Câu 2:
Đặt \(\widehat{D}=a;\widehat{E}=b\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=52\\a+b=140\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=96\\b=44\end{matrix}\right.\)
Bài 3:
Theo đề, ta có: x+2x+3x=180
=>6x=180
=>x=30
=>\(\widehat{A}=30^0;\widehat{B}=60^0;\widehat{C}=90^0\)

4 góc tứ giác là a,b,c,d
=.4 góc ngoài =180-a,180-b,180-c,180-d
=>tổng chúng =720độ - 360 độ=360 độ
Gọi 4 góc của tứ giác là : a , b , c , d
Thì 4 góc ngoài của tứ giác lần lượt là : 180 - a ; 180 - b ; 180 - c ; 180 - d
Vậy 4 góc ngoài của tứ giác là : 180 - a + 180 - b + 180 - c + 180 - d
= ( 180 + 180 + 180 + 180 ) - ( a + b + c + d )
= 720o - 360o ( tổng 4 góc của tứ giác )
= 360o
Vậy tổng 4 góc ngoài của tứ giác là 360o
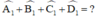
Mỗi góc ngoài của một tam giác bằng tổng của hai góc trong không kề với nó.
180 độ là sai mk thử rùi