Tìm hệ số của x5 trong khai triển P(x)=(1+x)+2(1+x)2+ … + 8(1+x)8
A. 630
B. 635
C. 636
D. 637
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
21 tháng 9 2018
Đúng(0)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
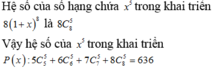
Câu 8 là \(\left(8a^2-\dfrac{1}{2}b\right)^6\) hay \(\left(8a^2-\dfrac{1}{2b}\right)^6\) bạn? (tốt nhất là bạn dùng tính năng gõ công thức toán để đăng đề, hoặc chụp hình gửi đề trực tiếp lên, hiện nay hoc24 đã cho đăng đề bằng hình ảnh)
9.
\(\left(x+8.x^{-2}\right)^9=\sum\limits^9_{k=0}C_9^kx^{9-k}.8^k.x^{-2k}=\sum\limits^9_{k=0}C_9^k8^kx^{9-3k}\)
Số hạng ko chứa x \(\Rightarrow9-3k=0\Rightarrow k=3\)
Số hạng đó là: \(C_9^3.8^3=...\)
CM
28 tháng 4 2018
Chọn D
Số hạng tổng quát của khai triển 
Số hạng chứa
x
5
trong A(x) là
Số hạng tổng quát của khai triển 
Số hạng chứa
x
5
trong B(x) là 
Vậy hệ số của số hạng chứa x 5 trong khai triển P(x) đã cho là 240-13608 = -13368.
HT
12 tháng 12 2020
15/ Mũ 4=> có 4+1=5 số hạng=> số hạng chính giữa là: \(C^2_4.3^{4-2}.x^2.2^2y^2=58x^2y^2\)
18/ \(x.x^k=x^7\Rightarrow k=6\)
\(C^6_9.3^6.2^3=489888\)
19/ \(C^7_7+C^7_8.\left(-1\right)^7+C^7_9.2^2=...\)
13 tháng 12 2020
C18 , c19 là lm sao vậy ạ ? Mk ko hiểu 2 bài này nơi
DG
2
B
3 tháng 9 2021
Đặt A=(2+x)5(3x-1)7
khai triển ta có:A=(\(_{k=0}^5\Sigma C_5^k2^{5-k}x^k\)).(\(^7_{i=0}\Sigma C_7^i\left(3x\right)^i\))
=\(\left(_{k=0}^5\Sigma\right)\left(_{i=0}^7\Sigma\right)\left(C_5^kC^i_7\right)\left(x^k.\left(3x\right)^i\right)\)
=số hạng\(\left(C_5^kC^i_7\right)\left(x^k.\left(3x\right)^i\right)\)chứa x5 tại k+i=5
có k\(\in\){0,1,2,...5},i\(\in\){0,1,2,...7}
=>(k,i)={(0,5);(1,4);(2,3);(3,2);(4,1);(5,0)}
=>Hệ số của x5 là:\(\left(C_5^0C^5_7\right)3^5\)+\(\left(C_5^1C^4_7\right)\left(3^4\right)\)+\(\left(C_5^2C^3_7\right)\left(3^3\right)\)+\(\left(C_5^3C^2_7\right)\left(3^2\right)\)+
\(\left(C_5^4C^1_7\right)\left(3^1\right)\)+\(\left(C_5^5C^0_7\right)3^0\)=30724
Hok tốt!!!
PT
1
PT
1
CM
1 tháng 3 2018
Đáp án C
Phương pháp:
Phân tích đa thức 1 + x + x 2 + x 3 thành nhân tử.
Sử dụng khai triển nhị thức Newton:
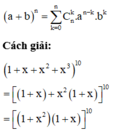
Áp dụng khai triển nhị thức Newton ta có:
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 11 2019
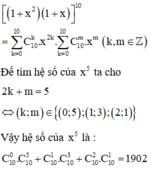
Làm xong rồi nhấn gửi thì lỗi, làm lại từ đầu nên chỉ làm 2 câu thôi, 2 câu sau bạn tự làm tương tự:
a/ \(\sum\limits^8_{k=0}C_8^kx^{2k}\left(1-x\right)^k=\sum\limits^8_{k=0}\sum\limits^k_{i=0}C_8^kC_k^i\left(-1\right)^ix^{2k+i}\)
Số hạng chứa \(x^8\) có:
\(\left\{{}\begin{matrix}2k+i=8\\0\le i\le k\le8\\i;k\in N\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(0;4\right);\left(2;3\right)\)
Hệ số: \(C_8^4C_4^0.\left(-1\right)^0+C_8^3C_3^2.\left(-1\right)^2\)
b/ \(1+x+x^2+x^3=\left(1+x\right)\left(1+x^2\right)\)
\(\Rightarrow\left(1+x+x^2+x^3\right)^{10}=\left(1+x\right)^{10}\left(1+x^2\right)^{10}\)
\(=\sum\limits^{10}_{k=0}C_{10}^kx^k\sum\limits^{10}_{i=0}C_{10}^ix^{2i}=\sum\limits^{10}_{k=0}\sum\limits^{10}_{i=0}C_{10}^kC_{10}^ix^{2i+k}\)
Số hạng chứa \(x^5\) có:
\(\left\{{}\begin{matrix}2i+k=5\\0\le k\le10\\0\le i\le10\\i;k\in N\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(0;5\right);\left(1;3\right);\left(2;1\right)\)
Hệ số: \(C_{10}^0C_{10}^5+C_{10}^1C_{10}^3+C_{10}^2C_{10}^1\)