Có bao nhiêu giá trị nguyên của tham số m để hàm số y = 1 3 x 3 - 2 m x 2 + 4 x - 5 đồng biến trên ℝ .
A. 0
B. 2
C. 3
D. 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 7 2021
3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)
CM
13 tháng 11 2019
Chọn D.
Ta có: y = x + m x 2 + 2
⇒ y ' = 1 + m x x 2 + 2
Hàm số đã cho đồng biến trên ℝ
và f ' x = 0 tại hữu hạn điểm.
+) Với x = 0 ⇒ y ' ≥ 0 ∀ m ⇒ t m
+) Với x > 0 ta có: (*)
+) Với x < 0 ta có: (*)
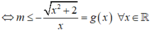
Xét g x = - x 2 + 2 x x # 0 t a c ó :
g ' x = 2 x 2 x 2 + 2 > 0 ∀ x ∈ ℝ
⇒ Hàm số đồng biến trên trên - ∞ ; 0 v à 0 ; + ∞
BBT:
Từ BBT ta được: - 1 ≤ m ≤ 1 thỏa mãn bài toán
Mà m ∈ ℤ ⇒ m ∈ - 1 ; 0 ; 1
CM
14 tháng 2 2017
Chọn D
Phương pháp:
Sử dụng: Hàm số y = ax+b đồng biến ⇔ a > 0, từ đó kết hợp điều kiện đề bài để tìm các giá trị của m.
Cách giải:
Hàm số y = (m-2)x + 2 đồng biến trên ℝ ⇔ m - 2 > 0 ⇔ m > 2
Mà 
=> có 2016 giá trị nguyên của m thỏa mãn đề bài.
CM
13 tháng 12 2019
Chọn đáp án D
* Với m - 1 = 0 ⇔ m = 1 thì hàm số đã cho trở thành y = x + 1
Hàm số này có đồ thị là một đường thẳng và hàm số luôn đồng biến trên ℝ
* Với m - 1 ≠ 0 ⇔ m ≠ 1 thì hàm số đã cho là một hàm số bậc ba có đạo hàm là
Do phương trình y ' = 0 có nhiều nhất hai nghiệm trên ℝ nên để hàm số đồng biến trên ℝ
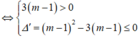
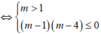
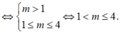
Do m ∈ ℤ nên m ∈ 2 ; 3 ; 4
Vậy có 4 giá trị m nguyên để hàm số đã cho đồng biến trên ℝ là m ∈ 1 ; 2 ; 3 ; 4
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1 2022
\(y'=x^2-2\left(m-1\right)x+3\left(m-1\right)\)
Hàm đồng biến trên khoảng đã cho khi với mọi \(x>1\) ta luôn có:
\(g\left(x\right)=x^2-2\left(m-1\right)x+3\left(m-1\right)\ge0\)
\(\Rightarrow\min\limits_{x>1}g\left(x\right)\ge0\)
Do \(a=1>0;-\dfrac{b}{2a}=m-1\)
TH1: \(m-1\ge1\Rightarrow m\ge2\)
\(\Rightarrow g\left(x\right)_{min}=f\left(m-1\right)=\left(m-1\right)^2-2\left(m-1\right)^2+3\left(m-1\right)\ge0\)
\(\Rightarrow\left(m-1\right)\left(4-m\right)\ge0\Rightarrow1\le m\le4\Rightarrow2\le m\le4\)
TH2: \(m-1< 1\Rightarrow m< 2\Rightarrow g\left(x\right)_{min}=g\left(1\right)=m\ge0\)
Vậy \(0\le m\le4\)
CM
3 tháng 6 2018
Chọn B
Phương pháp:
Tính y'.
Tìm m để 
Cách giải:
Ta có 
Xét phương trình y' = 0 
có 
Suy ra phương trình y' = 0 luôn có hai nghiệm 
Dễ thấy 
trong khoảng 
thì hàm số đồng biến.
Bài toán thỏa 
Do 
Vậy có 
giá trị của m thỏa mãn bài toán.
Chú ý:
Cách khác: Tìm m để 
Theo định lí Viet, ta có 
Hàm số đồng biến trên
(
2
;
+
∞
)
⇔
phương trình y' = 0 có hai nghiệm 
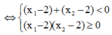
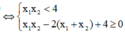
Vậy có 1001 số nguyên m thuộc khoảng (-10000;10000)
Đáp án là C