Cho tam giác ABC vuông tại A có ba cạnh CA, AB, BC lần lượt tạo thành một cấp số nhân có công bội q. Tìm q ?
A. 5 − 1 2
B. 2 + 2 5 2
C. 1 + 5 2
D. 2 5 − 2 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có
A M 2 + B C 2 2 = A B 2 B C . A B = A M 2 ⇒ B C . A B + B C 2 2 = A B 2 ⇔ A B B C 2 − A B B C − 1 4 = 0
⇔ q 2 = A B B C = 1 + 2 2 ⇔ q = 1 + 2 2

Chọn đáp án B
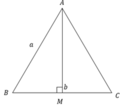
A B = a , B C = b ⇒ A M = a 2 - b 2 4
độ dài cạnh BC, trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành một cấp số nhân
![]()
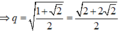

Đáp án B
Đặt B C = 2 x ⇒ A M = 2 q x , A B = 2 q 2 x .
Ta có: A B 2 = A M 2 + B M 2 ⇔ 2 q 2 x 2 = 2 q x 2 + x 2 ⇔ 4 q 4 − 4 q 2 − 1 = 0 ⇒ q 2 = 2 + 2 2 4
⇒ q = 2 + 2 2 2 .

Theo giả thiết AB=AC, BC,AH,AB lập thành cấp số nhân nên ta có hệ:
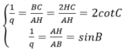
Từ đó ta có kết quả sau: 2cotC = sinC ⇔ 2cosC =sin2C = 1-cos2C
⇔ cos2C + 2cosC -1 =0 ⇒cosC = -1 +√2 (0° < C < 90°)
Do C là góc nhọn nên :
![]()
Cho nên công bội của cấp số nhân là:
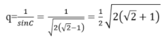
Đáp án C.

Đáp án B
Theo giả thiết AB = AC và BC, AH, AB theo thứ tự lập thành một cấp số nhân nên ta có hệ
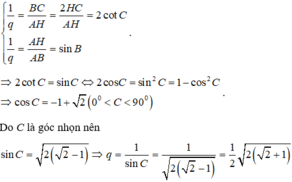
Đáp án B
Ta có A C . B C = A B 2 ⇔ A C . B C = B C 2 − A C 2 ⇔ A C 2 q 2 = A C 2 q 4 − A C 2 ⇒ q 2 = q 4 − 1
⇔ q 2 = 1 + 5 2 q 2 = 1 − 5 2 ⇒ q 2 = 1 + 5 2 ⇒ q = 1 + 5 2 = 2 + 2 5 2 .