cho 5a2+2b2=11ab với a>b/5>0
tính giá trị của biểu thức A=(4a2-5b2)/(a2+3ab)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MC
0
CM
9 tháng 8 2018
a − b = 29 + 12 5 − 2 5 = 3 + 2 5 2 − 2 5 = 3 A = a 3 − b 3 + a 2 + b 2 − 11 a b + 2015 = ( a − b ) ( a 2 + b 2 + a b ) + a 2 + b 2 − 11 a b + 2015 = 3 ( a 2 + b 2 + a b ) + a 2 + b 2 − 11 a b + 2015 = 4 ( a 2 − 2 a b + b 2 ) + 2015 = 4 a - b 2 + 2015 = 2051
CM
25 tháng 3 2019
Giả sử phương trình đã cho có 3 nghiệm
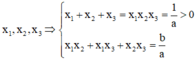
Khi đó
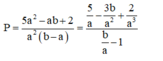
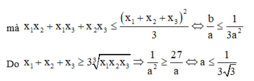
Suy ra
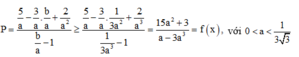
Xét hàm số:
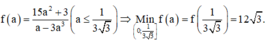
Chọn D.
23 tháng 12 2021
M=a3+b3+3ab(a2+b2)+6a2b2(a+b)
M=a3+b3+3ab(a2+b2)+6a2b2(a+b)
=(a+b)(a2−ab+b2)+3ab[(a+b)2−2ab]+6a2b2(a+b)
=(a+b)(a2−ab+b2)+3ab[(a+b)2−2ab]+6a2b2(a+b)
=(a+b)[(a+b)2−3ab]+3ab[(a+b)2−2ab]+6a2b2(a+b)
=(a+b)[(a+b)2−3ab]+3ab[(a+b)2−2ab]+6a2b2(a+b)
Thay a + b = 1 vào biểu thức trên ,có :
1.(12−3ab)+3ab(12−2ab)+6a2b2.11.(12−3ab)+3ab(12−2ab)+6a2b2.1
=1−3ab+3ab−6a2b2+6a2b2=1=1−3ab+3ab−6a2b2+6a2b2
=1
Vậy biểu thức M có giá trị bằng 1 khi a + b = 1
TD
2
DS
Đinh Sơn Tùng
CTVHS
VIP
23 tháng 11 2023
Ta có: a + b = 1
M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b)
= (a + b)3 - 3ab(a + b) + 3ab[(a + b)2 - 2ab] + 6a2 b2 (a + b)
= 1 - 3ab + 3ab(1 - 2ab) + 6a2 b2
= 1 - 3ab + 3ab - 6a2 b2 + 6a2 b2
= 1
nhwos tick nha :D
KT
1
7 tháng 11 2023
M=(a+b)(a2-ab+b2)+3ab(1-2ab)+6a2b2
M=a2-ab+b2+3ab
M=(a+b)2=1
