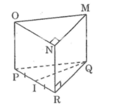
Quan sát hình lăng trụ đứng. Các phát biểu sau đây đúng hay sai?
a, Các cạnh MQ và MO vuông góc với nhau.
b. MQ vuông góc QI(I là trung điểm của PR).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Từ hình khai triển bên, ta có thể gấp theo các cạnh để được hình lăng trụ đứng.
b) Các phát biểu đúng:
- Cạnh AD vuông góc với cạnh AB.
- EF và CF là hai cạnh vuông góc với nhau.
- Hai đáy (ABC) và (DEF) nằm trên hai mặt phẳng song song với nhau.

a) Từ hình khai triển bên, ta có thể gấp theo các cạnh để được hình lăng trụ đứng.
b) Các phát biểu đúng:
- Cạnh AD vuông góc với cạnh AB.
- EF và CF là hai cạnh vuông góc với nhau.
- Hai đáy (ABC) và (DEF) nằm trên hai mặt phẳng song song với nhau.

a. Sai vì AB không phải là cạnh bên.
b. Sai vì EF không phải là cạnh bên.
c. Sai vì AC và DF không phải là cạnh bên và không vuông góc.
d. Sai vì AC và DF không phải là cạnh bên.
e. Đúng vì mp (ABC) // mp (DEP).
f. Sai vì mp (ACFD) và mp (BCFE) cắt nhau.
g. Đúng vì mp (ABED) và mp (DEP) vuông góc với nhau

a) Hình 7a: Mặt đáy: ABC và DEF
Mặt bên: ABED, BCFE, ACFD
Hình 7b: Mặt đáy: ABCD, MNPQ
Mặt bên: ABNM, BCPN, CDQP, ADQM.
b) Ở Hình 7a, cạnh BE = AD = CF
Ở Hình 7b, cạnh MQ = NP = BC = AD

a) Các cạnh song song với nhau là: AD và BC
b) Các cạnh góc vuông với nhau là: AD và AB; BA và BC
c) Góc vuông đỉnh A; cạnh AD, AB
Góc vuông đỉnh B; cạnh BA, BC
Góc nhọn đỉnh D; cạnh DA, DC
Góc tù đỉnh C, cạnh CB, CD

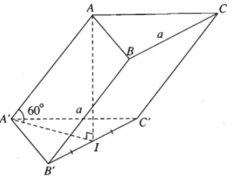
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
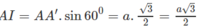
b) 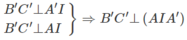
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.
Ta có hình lăng trụ đứng MNO.QRP.
a. Vì mặt bên (MOPQ) là một hình chữ nhật nên MQ ⊥ MO.
Vậy phát biểu a đúng.
b. Vì MQ ⊥ (QRP) nên MQ ⊥ QL
Vậy phát biểu b đúng.