Cho hàm số y = - 0 , 75 x 2 . Qua đồ thị của hàm số đó, hãy cho biết khi x tăng từ -2 đến 4 thì giá trị nhỏ nhất và giá trị lớn nhất của y là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = -0,75x2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
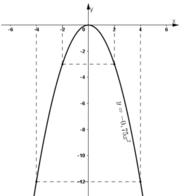
- Quan sát đồ thị hàm số y = -0,75x2:
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.

Vẽ đồ thị: y = -0,75x2
| x | -4 | -2 | -1 | 0 | 1 | 2 | 4 |
| y=-0,75x2 | -12 | -3 | -0,75 | 0 | -0,75 | -3 | -12 |
Vì -2 < 0 < 4 và khi x = 0 thì y = 0 là giá trị lớn nhất của hàm số. Hơn nữa khi x = -2 thì y = -0,75 . (-2)2 = -3, khi x = 4 thì y = -0,75 . (4)2 = -12 < -3
Do đó khi -2 ≤ x ≤ 4 thì giá trị nhỏ nhất của hàm số là -12 còn giá trị lớn nhất là 0.

Vẽ hình:
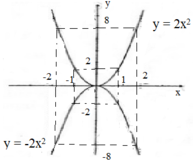
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.

Vẽ hình:
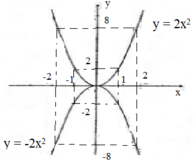
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.

Chọn A
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
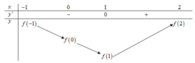
Nhận thấy
![]()
Để tìm ![]() ta so sánh f(-1) và f(2)
ta so sánh f(-1) và f(2)
Theo giả thiết, ![]()
![]()
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 ![]()
![]()

Chọn B
Ta có:
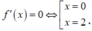
biến thiên của hàm số f(x) trên đoạn [0;4]
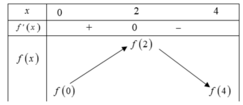
Nhìn vào bảng biến thiên ta thấy ![]()
Ta có f(2) + f(4) = f(3) + f(0) ⇔ f(0) - f(4) = f(2) - f(3) > 0.
Suy ra: f(4) < f(0). Do đó ![]()
Vậy giá trị nhỏ nhất và lớn nhất của f(x) trên đoạn [0;4] lần lượt là: f(4), f(2).

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3

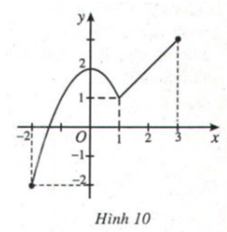
Giá trị nhỏ nhất của hàm số trên đoạn [-2,3] là điểm thấp nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị nhỏ nhất tại x = -2. Thay x = -2 vào hàm số y đã cho ta có giá trị nhỏ nhất là -2.
Giá trị lớn nhất của hàm số trên đoạn [-2,3] là điểm cao nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị lớn nhất tại x = 3. Thay x = 3 vào hàm số y đã cho ta có giá trị lớn nhất là 3.
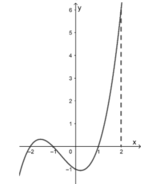
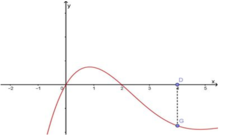
- Lập bảng giá trị:
- Vẽ đồ thị:
- Quan sát đồ thị hàm số y = - 0 , 75 x 2 :
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.