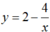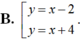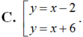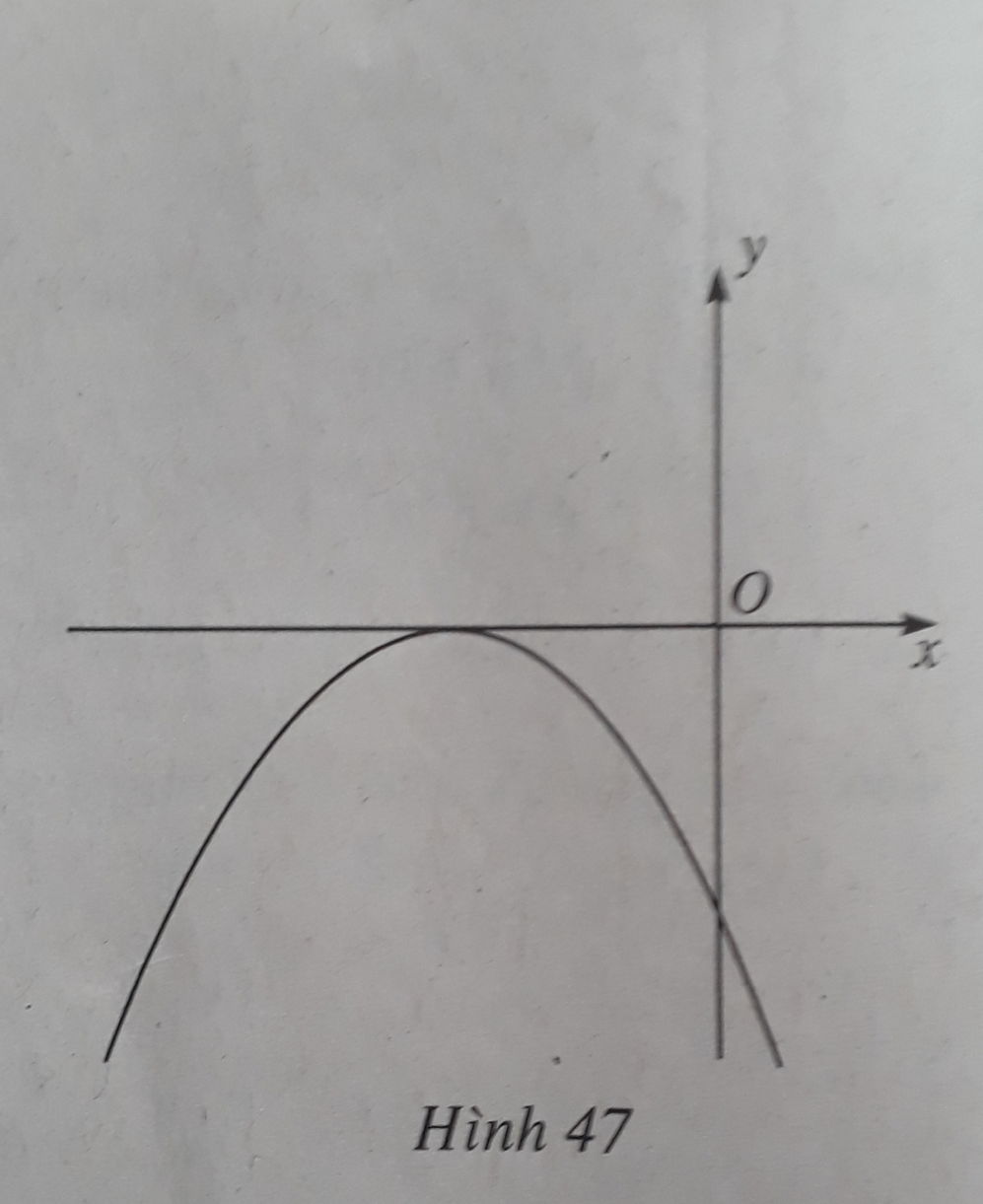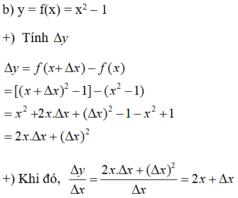Tính Δ y và ∆ y ∆ x của các hàm số sau theo x và Δ x : y = 1 x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
29 tháng 9 2018
Đúng(0)
Những câu hỏi liên quan
VT
23 tháng 8 2019
Đáp án A
Đặt
Đặt
Vậy tính bền vững của hạt nhân giảm dần theo thứu tự Y,X,Z
1 tháng 4 2018
mk chỉ cho cách lm ; bn tự lm cho bt nha
câu a : lập bảng sét dấu tìm được \(x\) để \(y>0;y< 0\)
tiếp là đưa nó về dạng bình phương 1 số cộng 1 số \(\left(n^2+m\right)\) rồi tìm \(y_{min}\)
câu b : giao điểm của \(\left(P\right)\) và đường thẳng \(\left(d\right):y=2x+1\)
là nghiệm của hệ phương trình : \(\left\{{}\begin{matrix}y=x^2-2x-1\\y=2x+1\end{matrix}\right.\)
CM
9 tháng 4 2019
Chọn C.
Đạo hàm: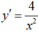 
Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 nên có hệ số góc bằng 1.
Ta có phương trình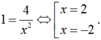 
Tại M(2; 0). Phương trình tiếp tuyến là y = x – 2.
Tại N(-2; 4). Phương trình tiếp tuyến là y = x + 6.
PT
1
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Thay x vào ta có:
Dựa vào bảng trên ta thấy:
Khi x tăng, giá trị y của hàm số y=-x+1 giảm
Khi x tăng, giá trị y của hàm số y=x tăng
biến đường thẳng Δ: x - y -1 = 0 thành đường thẳng Δ' có phương trình là
24 tháng 10 2016
Giải:
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{A}+\widehat{B}+30^o=180^o\)
\(\Rightarrow\widehat{A}+\widehat{B}=150^o\)
a) Ta có: \(\widehat{A}+\widehat{B}=150^o\)
\(\Rightarrow x+y=150^o\)
Mà x = 2y
\(\Rightarrow2y+y=150^o\)
\(\Rightarrow3y=150^o\)
\(\Rightarrow y=50^o\)
\(\Rightarrow x=50^o.2=100^o\)
Vậy \(y=50^o,x=100^o\)
b) Ta có: \(\widehat{A}+\widehat{B}=150^o\)
\(\Rightarrow x+y=150^o\)
Mà \(x-y=10^o\)
\(\Rightarrow x=\left(150^o+10^o\right):2=80^o\)
\(\Rightarrow y=150^o-80^o=70^o\)
Vậy \(x=80^o,y=70^o\)
c) Ta có: \(3x=2y\Rightarrow\frac{x}{3}=\frac{y}{2}\) và \(\widehat{A}+\widehat{B}=150^o\) hay \(x+y=150^o\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{2}=\frac{x+y}{3+2}=\frac{150^o}{5}=30^o\)
+) \(\frac{x}{3}=30^o\Rightarrow x=90^o\)
+) \(\frac{y}{2}=30^o\Rightarrow y=60^o\)
Vậy \(x=90^o,y=60^o\)
TA
17 tháng 6 2021
Gọi `A(0;1)` và `B(1;3)` là 2 điểm thuộc `\Delta`
`T_(\vec v): \Delta -> \Delta'`
`<=> T_(\vec v): A(0;1) -> A'(3;0) ; B(1;3) -> B'(4;2)`
`=> \vec(A'B') (1;2)`
`=> \Delta' : 1(x-3)+2(y-0)=0 <=> x+2y-3=0`
`(C)` có: `I(1;-2)` và `R=\sqrt6 =R'`
`T_(\vec v): (C) -> (C') => T_(\vecv): I (1;-2) -> I'(4;-3)`
`=> (C'): (x-4)^2 +(y+3)^2=6`