Có N 1 bóng đèn cùng loại 3 V - 3 W và N 2 nguồn điện có cùng suất điện động E 0 = 4 V và điện trở trong r 0 = 1 Ω được mắc thành bộ nguồn hỗn hợp đối xứng. Nếu số bóng đèn là N 1 = 8 thì cần số nguồn ít nhất ( N 2 min) là bao nhiêu để các đèn này sáng bình thường ? Vẽ sơ đồ các cách mắc nguồn và đèn khi đó và tính hiệu suất của bộ nguồn trong từng trường hợp.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
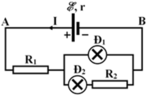
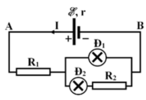
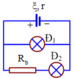
R Đ 1 = 12 Ω, R Đ 2 = 5 Ω, I Đ M 1 = I 1 = 0,5 A, I Đ M 2 = I 2 = 0,5 A
Để 2 đèn sáng bình thường thì U 1 = U 2 = 6 V
![]()
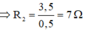
Dòng điện chạy trong mạch chính I = 0,5 + 0,5 = 1 A
Ta có:
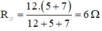
Mặt khác:
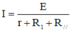
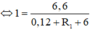
![]()
![]()

Đáp án C
Ta có :
![]()
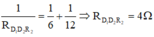
![]()
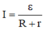
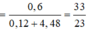
![]()
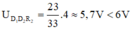
Suy ra Đèn 1 sáng yếu hơn đèn bình thường
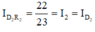
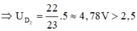
Suy ra Đèn 2 sáng hơn đèn bình thường

đáp án D
P d = I d 2 R d = U d 2 R d ⇒ R d = U d 2 P d = 6 2 6 = 6 Ω
ξ b = 4 ξ = 6 V r b = 4 r 2 = 2 Ω ⇒ I = ξ R d + r b = 6 6 + 2 = 0 , 75 A ⇒ P n g = ξ b I = 4 , 5 W P = I 2 R d = 3 , 375 W U = I . R d = 4 , 5 V
+ Công suất của mỗi nguồn:
P i = P n g 8 = 0 , 5625 W
+ Hiệu điện thế giữa hai cực của mỗi nguồn:
U i 4 = U 4 = 1 , 125 V

Nếu số nguồn là N 2 = mn = 15 và với số đèn là N 1 = xy ta cũng có phương trình (1) và bất đẳng thức (2) trên đây. Kết quả là trong trường hợp này ta có :
3yn + xm = 4mn ≥ 2. 3 m n x y hay 60 ≥ 2. 45 N 1
Từ đó suy ra : N 1 ≤ 20. Vậy với~số nguồn là N 2 = 15 thì có thể thắp sáng bình thường số đèn lớn nhất là N 1 = 20.
Để tìm được cách mắc nguồn và đèn trong trường hợp này ta có xỵ = 20 hay y = 20/x. Thay giá trị này vào phương trình (1) ta đi tới phương trình :
m x 2 – 60x + 60n = 0
Phương trình này có nghiêm kép ( ∆ ' = 0) là : x = 30/m.
Chú ý rằng x, y, n và m đều là số nguyên, dương nên ta có bảng các trị số này như sau :
| m | n | x | y |
| 3 | 5 | 10 | 2 |
| 15 | 1 | 2 | 10 |
Như vậy trong trường hợp này chỉ có hai cách mắc các nguồn và các bóng đèn là :
- Cách một : Bộ nguồn gồm n = 5 dãy song song, mỗi dãy gồm m - 3 nguồn mắc nối tiếp và các bóng đèn được mắc thành X - 10 dãy song song với mỗi dãy gồm y - 2 bóng đèn mắc nối tiếp (Hình 11.6Ga).
Cách mắc này có hiệu suất là : H 1 = 6/12 = 50%
- Cách hai : Bộ nguồn gồm n = 1 dãy có m = 15 nguồn mắc nối tiếp và các bóng đèn được mắc thành x = 2 dãy song song với mỗi dãy gồm y = 10 bóng đèn mắc nối tiếp (Hình 11.6Gb).
Cách mắc này có hiệu suất là : H 2 = 30/60 = 50%

Vì các bóng đèn cùng loại nên phải được mắc thành các dãy song song, mỗi dãy gồm cùng số đèn mắc nối tiếp. Bằng cách đó, dòng điện chạy qua mỗi đèn mới có cùng cường độ bằng cường độ định mức. Giả sử các đèn được mắc thành x dãy song song, mỗi dãy gồm y đèn mắc nối tiếp theo sơ đồ như trên Hình 11.1G.
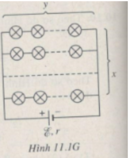
Các trị số định mức của mỗi đèn là :
U đ = 6V; P đ = 3 W ; I đ = 0,5 A.
Khi đó hiệu điện thế mạch ngoài là : U = y U đ = 6y.
Dòng điện mạch chính có cường độ là :
I = x I đ = 0,5x
Theo định luật Ôm ta có : U = E - Ir, sau khi thay các trị số đã có ta được :
2y + x = 8 (1)
Kí hiệu số bóng đèn là n = xy và sử dụng bất đẳng thức Cô-si ta có :
2y + x ≥ 2. x y (2)
Kết hợp (1) và (2) ta tìm được : n = xy ≤ 8.
Vậy có thể mắc nhiều nhất là n = 8 bóng đèn loại này.
Dấu bằng xảy ra với bất đẳng thức (2) khi 2y = x và với xy = 8. Từ đó suy ra x = 4 và y = 2, nghĩa là trong trường hợp này phải mắc 8 bóng đèn thành 4 dãy song song, mỗi dãy gồm 2 bóng đèn mắc nối tiếp như sơ đồ Hình 11.2G.
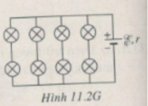

đáp án B
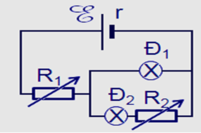
P d = I d 2 R d = U d 2 R d ⇒ R d = U d 2 P d R d 1 = 12 2 6 = 24 R d 2 = 6 2 4 , 5 = 8 ⇒ R = R d 1 R b + R d 2 R d 1 + R b + R d 2 = 9 , 6
⇒ I = ξ R + r = 12 9 , 6 + 0 , 4 = 1 , 2 A H = R R + r = 9 , 6 9 , 6 + 0 , 4 = 0 , 96 P m g = ξ I = 12 . 1 , 2 = 14 , 4 W



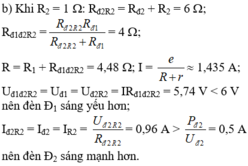

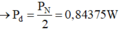
Để các đèn cùng loại sáng bình thường thì các đèn thành các dãy song song, mỗi dãy có cùng một số đèn mắc nối tiếp. Gọi số dãy các đèn mắc song song là x và số đèn mắc nối tiếp là y thì theo đầu bài ta xét trường hợp có tổng số đèn là : N 1 = xy = 8.
Giả sử bộ nguồn hỗn hợp đối xứng gồm n dãy song song và mỗi dãy gồm m nguồn được mắc nối tiếp (Hình 11.4G). Khi đó bộ nguồn gồm N 2 = mn nguồn và có suất điện động là : E b = m E 0 = 4m và có điện trở trong là
r b = m r 0 /n = m/n
Các trị số định mức của đèn là : U Đ = 3 V ; P Đ = 3 W do đó I Đ = 1 A.
Cường độ dòng điện mạch chính là :
I = x I Đ = x
Hiệu điện thế mạch ngoài là : U = y U Đ = 3ỵ.
Theo định luật Ôm ta có : U = E b – I r b hay 3y = 4m - x.m/n
Từ đó suy ra 3yn + xm = 4mn (1)
Sử dụng bất đẳng thức Cô-si ta có : 3yn + xm ≥ 2. 3 m n x y (2)
Kết hợp (1) và (2) trong đó chú ý là N 1 = xy = 8 và N 2 = mn ta tìm được: N 2 ≥ 6; y = N 1 /x = 8/x
Vậy số nguồn ít nhất tà N 2 (min) = 6 để thắp sáng bình thường bóng đèn.
Để vẽ được sơ đồ các cách mắc nguồn và đèn cho trường hợp này ta lại xét phương trình (1) trên đây, trong đó thay trị số N 2 = mn = 6; y =
ta đi tới phương trình : y n 2 – 8n + 2x = 0
Phương trình này có nghiệm kép ( ∆ ’ = 0) là : n = 4/y
Chú ý rằng x, y, n và m đều là số nguyên, dương nên ta có bảng các trị số này như sau :
Như vậy trong trường hợp này chỉ có hai cách mắc các nguồn và các bóng đèn là
- Cách một : Bộ nguồn gồm n = 2 dãy song song, mỗi dãy gồm m = 3 nguồn mắc nối tiếp và các bóng đèn được mắc thành x = 4 dãy song song với mỗi dãy gồm y = 2 bóng đèn mắc nối tiếp (Hình 11.5Ga).
Cách mắc này có hiệu suất là : H 1 = 6/12 = 50%
- Cách hai : Bộ nguồn gồm n = 1 dãy gồm m = 6 nguồn mắc nối tiếp và các bóng đèn được mắc thành X = 2 dãy song song với mỗi dãy gồm y = 4 bóng đèn mắc nối tiếp (Hình 11.5Gb).
Cách mắc này có hiệu suất là : H 2 = 12/24 = 50%