Mạch điện xoay chiều gồm có: R = 30Ω,C =
1
5000
π
F, L =
0
,
2
π
H . Biết điện áp tức thời hai đầu mạch u = 120
2
cos100πt (V). Viết biểu thức của i. A. i = 2cos(100πt +
π
4
) (A) B. i = 2
2
cos(100πt +
π
4
) (A) C. i = 4cos(100πt +
π
4
) (A) D. i = 4cos(100πt +
π
2
)...
Đọc tiếp
Mạch điện xoay chiều gồm có: R = 30Ω,C = 1 5000 π F, L = 0 , 2 π H . Biết điện áp tức thời hai đầu mạch u = 120 2 cos100πt (V). Viết biểu thức của i.
A. i = 2cos(100πt + π 4 ) (A)
B. i = 2 2 cos(100πt + π 4 ) (A)
C. i = 4cos(100πt + π 4 ) (A)
D. i = 4cos(100πt + π 2 ) (A)
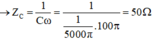
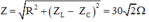
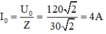
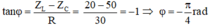
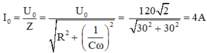
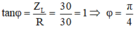
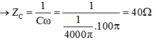
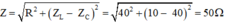
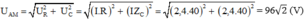
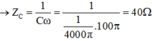
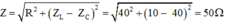
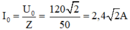
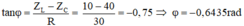
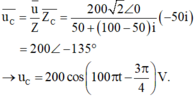
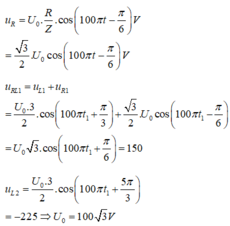
Chọn C
Áp dụng các công thức: ZC = 1 C ω = 50 Ω; ZL = ωL = 20 Ω
⇒ Z = R 2 + ( Z L - Z C ) 2 = 30 2 Ω
Cường độ dòng điện hiệu dụng: I = U : Z = 120 : 30 2 = 4 2 A
Độ lệch pha:
tan φ = Z L - Z C R = - 1 ⇒ φ = π 4
Tức là i sớm pha hơn u một góc π 4 .
Vậy biểu thức tức thời của cường độ dòng điện là: i = 4cos(100πt + π/4) (A)