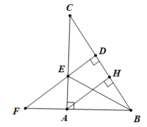
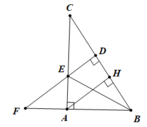
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC tại E, cắt BA tại F. Chứng minh
a. ΔABE = ΔBDE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 5 2019
A.Xét ΔABE và ΔDBE có:
Cạnh BE chung
BD = BA
⇒ ΔABE = ΔDBE (cạnh huyền – góc nhọn)
b. Do BD = BA nên B nằm trên đường trung trực của AD
Do ΔABE = ΔDBE ⇒ AE = ED (hai cạnh tương ứng)
E nằm trên đường trung trực của AD
Vậy BE là đường trung trực của AD
c. Do ΔABE = ΔDBE ⇒ ∠(ABE) = ∠(EBC) (hai góc tương ứng)
Suy ra BE là tia phân giác của góc ABC
CM
20 tháng 4 2018
c. Do ΔABE = ΔDBE ⇒ ∠(ABE) = ∠(EBC) (hai góc tương ứng)
Suy ra BE là tia phân giác của góc ABC (1 điểm)
CM
24 tháng 1 2018
b. Do BD = BA nên B nằm trên đường trung trực của AD
Do ΔABE = ΔDBE ⇒ AE = ED (hai cạnh tương ứng) (1 điểm)
E nằm trên đường trung trực của AD (1 điểm)
Vậy BE là đường trung trực của AD (0.5 điểm)
10 tháng 5 2023
a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
=>ΔBAE=ΔBDE
b; BA=BD
EA=ED
=>BE là trung trực của AD
26 tháng 3 2019
Bài này tớ nghĩ không cần điểm E đâu.v:))
Trên cạnh AC lấy điểm K sao cho AK=AH.
Do tam giác ABD cân tại B nên ^BAD=^BDA.
Ta có:\(\widehat{DAK}=\widehat{BAC}-\widehat{BAD}=90^0-\widehat{BAD}\)
\(\widehat{HAD}=\widehat{DHA}-\widehat{AHD}=90^0-\widehat{AHD}\)
\(\Rightarrow\widehat{DAK}=\widehat{HAD}\)
Xét \(\Delta\)HAD và \(\Delta\)KAD có:AD chung;^DAK=^HAD;AH=AK \(\Rightarrow\Delta HAD=\Delta KAD\left(c-g-c\right)\Rightarrow\widehat{AHD}=\widehat{AKD}=90^0\)
\(\Rightarrow\Delta CKD\) vuông tại K.\(\Rightarrow KD< DC\)(1)
Mà \(\Delta\)HAD = \(\Delta\)KAD nên HD=KD.(2)
Từ (1) và (2) suy ra điều cần chứng minh_._
.
1 tháng 4 2021
a) Ta có: \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy trong ΔBAC cân tại A)
mà \(\widehat{ACB}=\widehat{ECN}\)(hai góc đối đỉnh)
nên \(\widehat{ABC}=\widehat{ECN}\)
hay \(\widehat{MBD}=\widehat{NCE}\)
Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
DB=EC(cmt)
\(\widehat{MBD}=\widehat{NCE}\)(cmt)
Do đó: ΔMBD=ΔNCE(cạnh góc vuông-góc nhọn kề)
Suy ra: DM=EN(hai cạnh tương ứng)
9 tháng 5 2015
Tam giác ABC vuông tại A => góc ACD + DBA = 90o
Tam giác ABH vuông tại H => góc BAH + DBA = 90o
=> góc ACD = BAH
Xét tam giác ADC có: góc ADB = DAC + ACD (tính chất góc ngoài của tam giác)
=> góc ADB = DAC + BAH
mặt khác, Góc BAD = DAH + BAH
Vì tam giác ABD cân tại B (AB = AD) => góc ADB = BAD
=> DAC = DAH => AD là phân giác của góc HAC
a. Hình vẽ (0.5 điểm)
Xét ΔABE và ΔDBE có:
Cạnh BE chung
BD = BA
⇒ ΔABE = ΔDBE (cạnh huyền – góc nhọn) (1 điểm)