Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
=>ΔBAE=ΔBDE
b; BA=BD
EA=ED
=>BE là trung trực của AD

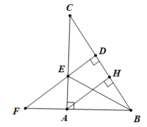
c. Do ΔABE = ΔDBE ⇒ ∠(ABE) = ∠(EBC) (hai góc tương ứng)
Suy ra BE là tia phân giác của góc ABC (1 điểm)

a. Hình vẽ (0.5 điểm)
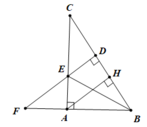
Xét ΔABE và ΔDBE có:
Cạnh BE chung
BD = BA
⇒ ΔABE = ΔDBE (cạnh huyền – góc nhọn) (1 điểm)

a, Xét tg BAE và tg BDE ( \(\widehat{BAE}=\widehat{BDE}=90^0\))
BA=BD (gt)
BE chung
=> tg BAE = tg BDE ( ch-cgv)
=> AE=ED
Ta có \(\hept{\begin{cases}BA=BD\left(gt\right)\\AE=ED\left(cmt\right)\end{cases}}< =>\)BE trung trực AD (đpcm)
b, +ED vuông BC
+ AH vuông BC
=> AH//DE
=> \(\widehat{HAD}=\widehat{ADE}\)( So le trong) (2)
Lại có gọi m là giao 2 đường thẳng BE và AD
vì BE trung trực AD =>+ \(\widehat{AME}=\widehat{EMD}=90^{0^{ }}\)
Xét tg AEM và tg DEM có \(\left(\widehat{AME}=\widehat{EMD}=90^0\left(cmt\right)\right)\)
+ AD = ED (cma)
+ EM chung
=> tg AEM = tg DEM ( ch-cgv)
=> \(\widehat{DAE}=\widehat{ADE}\)(2)
tỪ (1) VÀ (2) => \(\widehat{HAD}=\widehat{DAE}\)=> AD phân giác góc AHC

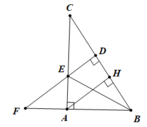
b. Do BD = BA nên B nằm trên đường trung trực của AD
Do ΔABE = ΔDBE ⇒ AE = ED (hai cạnh tương ứng) (1 điểm)
E nằm trên đường trung trực của AD (1 điểm)
Vậy BE là đường trung trực của AD (0.5 điểm)

a) ΔABDΔABD cân tại A => BADˆ=BDAˆBAD^=BDA^ (t/c tam giác cân)
Lại có: BADˆ+DAEˆ=BACˆ=90oBAD^+DAE^=BAC^=90o
BDAˆ+ADEˆ=BDEˆ=90oBDA^+ADE^=BDE^=90o
Do đó, DAEˆ=ADEˆDAE^=ADE^
=> ΔADEΔADE cân tại E (dấu hiệu nhận biết tam giác cân)
=> AE = ED (t/c tam giác cân) (đpcm)
a) Có: AH // ED (cùng ⊥BC⊥BC)
=> HADˆ=ADEˆHAD^=ADE^ (so le trong)
= DAE (câu a)
=> AD là phân giác HACˆ(đpcm)

Bài này tớ nghĩ không cần điểm E đâu.v:))
Trên cạnh AC lấy điểm K sao cho AK=AH.
Do tam giác ABD cân tại B nên ^BAD=^BDA.
Ta có:\(\widehat{DAK}=\widehat{BAC}-\widehat{BAD}=90^0-\widehat{BAD}\)
\(\widehat{HAD}=\widehat{DHA}-\widehat{AHD}=90^0-\widehat{AHD}\)
\(\Rightarrow\widehat{DAK}=\widehat{HAD}\)
Xét \(\Delta\)HAD và \(\Delta\)KAD có:AD chung;^DAK=^HAD;AH=AK \(\Rightarrow\Delta HAD=\Delta KAD\left(c-g-c\right)\Rightarrow\widehat{AHD}=\widehat{AKD}=90^0\)
\(\Rightarrow\Delta CKD\) vuông tại K.\(\Rightarrow KD< DC\)(1)
Mà \(\Delta\)HAD = \(\Delta\)KAD nên HD=KD.(2)
Từ (1) và (2) suy ra điều cần chứng minh_._