Mng giúp em với ak.Em đang cần...
Đọc tiếp
Mng giúp em với ak.Em đang cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
2
29 tháng 4 2022
a.\(A=\dfrac{1}{x-1}-\dfrac{x^2+x}{x^2+1}.\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\);\(ĐK:x\ne\pm1\)
\(A=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\left(\dfrac{x+1-x+1}{\left(x-1\right)\left(x+1\right)}\right)\)
\(A=\dfrac{1}{\left(x-1\right)}-\dfrac{2x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)\left(x^2+1\right)}\)
\(A=\dfrac{1}{x-1}-\dfrac{2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{x^2+1-2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{x-1}{x^2+1}\)
b.\(A=0,2=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{x-1}{x^2+1}=\dfrac{1}{5}\)
\(\Leftrightarrow x^2+1=5x-5\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
c.\(A< 0\) mà \(x^2+1\ge1>0\)
--> A<0 khi \(x-1< 0\)
\(\Leftrightarrow x< 1\)
29 tháng 4 2022
a. -ĐKXĐ:\(x\ne\pm1\)
\(A=\dfrac{1}{x-1}-\dfrac{x^2+x}{x^2+1}.\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\left(\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\dfrac{x+1-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\dfrac{2}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}\)
\(=\dfrac{x^2+1}{\left(x^2+1\right)\left(x-1\right)}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}\)
\(=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\)
b. \(A=\dfrac{x-1}{x^2+1}=0,2\)
\(\Leftrightarrow\dfrac{x-1}{x^2+1}=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{5\left(x-1\right)}{5\left(x^2+1\right)}=\dfrac{x^2+1}{5\left(x^2+1\right)}\)
\(\Rightarrow5x-5=x^2+1\)
\(\Leftrightarrow x^2-5x+1+5=0\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow x^2-2x-3x+6=0\)
\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=3\left(nhận\right)\end{matrix}\right.\)
c. \(A=\dfrac{x-1}{x^2+1}< 0\)
\(\Leftrightarrow x-1< 0\) (vì \(x^2+1>0\forall x\))
\(\Leftrightarrow x< 1\)
PT
1
2 tháng 11 2021
Câu 2:
a, Vì m⊥MN và n⊥MN nên m//n
b, Vì m//n nên \(\widehat{D_1}=\widehat{C}=45^0\) (so le trong)
c, Vì m//n nên \(\widehat{D_1}=\widehat{C_1}\) (đồng vị)
14 tháng 9 2021
a) Cường độ dòng điện I1 là:
Ta có: \(I_1=\dfrac{U_1}{R_1}=\dfrac{30}{15}=2\left(A\right)\)
Cường độ dòng điện I2 là:
Ta có: \(I_2=\dfrac{U_2}{R_2}=\dfrac{45}{30}=1,5\left(A\right)\)
Vì I1>I2 (2>1,5) mà R1 nt R2 thì chọn Imax = I1 = I2 = 1,5 A
b, Hiệu điện thế tối da là:
Ta có: \(U_{max}=I_{max}\left(R_1+R_2\right)=1,5.\left(15+30\right)=67,5\left(V\right)\)
VP
14 tháng 9 2021
a/ Cddd tối đa của R1: I1 = 30/15 = 2A; của R2: I2 = 45/30=1,5A
=> cddd tối đa của mạch là I2 = 1,5A
b/
U = I2.(R1+R2) = 67,5V
J
3
Y
28 tháng 6 2023
\(a,A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(=x-0,2-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(=\left(-0,2-2+2\right)+\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)\)
\(=-0,2\)
\(b,B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(=x^3-8y^3-x^3+8y^3-10\)
\(=-10\)
\(c,C=4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x-1\right)\left(x+1\right)-4x\)
\(=4\left(x^2+2x+1\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=13\)
H9
HT.Phong (9A5)
CTVHS
28 tháng 6 2023
a) \(A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(A=x-\dfrac{1}{5}-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(A=\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)-\left(\dfrac{1}{5}+2-2\right)\)
\(A=-\dfrac{1}{5}\)
Vậy: ...
b) \(B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(B=\left[x^3-\left(2y\right)^3\right]-\left[x^3-\left(2y\right)^3\right]-10\)
\(B=-10\)
Vậy: ...
c) \(4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x+1\right)\left(x-1\right)-4x\)
\(=4\left(x^2+2x+4\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=\left(4x^2+4x^2-8x^2\right)+\left(8x-4x-4x\right)+\left(4+1+8\right)\)
\(=13\)
Vậy:...
3 tháng 7 2021
1) \(A=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{x\sqrt{x}-1}:\dfrac{\sqrt{x}-1}{5}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{5}{\sqrt{x}-1}\) \(=\dfrac{5}{x+\sqrt{x}+1}\)
2) Ta thấy \(x+\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}+1\right)+1>1\forall x\)
\(\Rightarrow A< 5\)
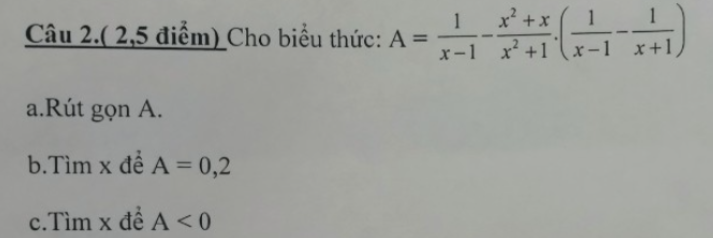
15 . C
16 . A
17 . A
18 . C
19 . B
20 . D
21 . A
22 .C
15. D
16. B
17. A
18. C
19. D
20. D
21. A
22. B
23. C