Người ta dựa 1cái thang sắt vào tường, chân thang cách chân tường 0,8m và đầu còn lại của thang chạm vào tường. Một người thợ leo lên thang và đứng ở bậc chính giữa của thang (vị trí chia đôi thang) để làm việc. Tính khoảng cách từ bậc thang người thợ đứng đến bức tường.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

35dm=3,5m
Chiều cao của bức tường là:
\(\sqrt{3.5^2-0.8^2}\simeq3,41\left(m\right)\)

Khoảng cách "an toàn" từ chân tường đến chân thang là: 1,75m

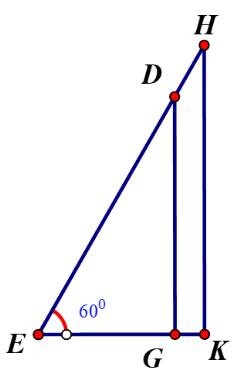
Gọi chiều cao bức tường DG là x (m) (x>0)
Chiều dài chiếc thang là x+1 (m)
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là: \(EG = \frac{{DG}}{{\sqrt 3 }} = \frac{{x\sqrt 3 }}{3}\) (m)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(BC = \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} \)(m)
Bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m nên ta có:
\(\sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} - 0,5 = \frac{{x\sqrt 3 }}{3}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} = \frac{x}{{\sqrt 3 }} + 0,5\\ \Leftrightarrow \sqrt {2x + 1} = \frac{x}{{\sqrt 3 }} + 0,5\left( * \right)\end{array}\)
Ta có \(\frac{x}{{\sqrt 3 }} + 0,5 \ge 0 \Leftrightarrow \frac{x}{{\sqrt 3 }} \ge - \frac{1}{2}\)\( \Leftrightarrow x \ge - \frac{{\sqrt 3 }}{2}\) (Luôn đúng do x>0)
Ta bình phương hai vế (*) ta được:
\(\begin{array}{l}2x + 1 = {\left( {\frac{x}{{\sqrt 3 }} + 0,5} \right)^2}\\ \Leftrightarrow 2x + 1 = \frac{{{x^2}}}{3} + \frac{x}{{\sqrt 3 }} + 0,25\\ \Leftrightarrow \frac{{{x^2}}}{3} + \left( {\frac{{\sqrt 3 }}{3} - 2} \right)x - \frac{3}{4} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x \approx 4,7\left( {tm} \right)\\x \approx - 0,5\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy chiều cao của bức tường là 4,7 m.

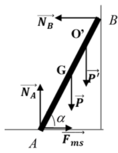
a. Trọng lượng của thanh: P = mg = 200N
Theo điều kiện cân bằng Momen
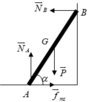
M P → = M N → B ⇒ P . A B 2 cos α = N B . A B . sin α
Theo điều kiện cân bằng lực
P → + N → A + N → B + F → m s = 0 → N A = P = 200 N ; F m s = N B ⇒ N B = F m s = P 2 = 100 N
b, Điều kiện: Fms <k.NA
Theo câu a F m s = N B = P 2 t g α
⇒ N A = P ⇒ t g α > 1 2 k = 1 1 , 2 ⇒ α = 40 0
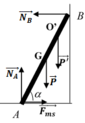
c. Lấy O’ là vị trí người khi thang bắt đầu trượt.
Ta có:
N B = F m s = k N A ; N A = P + P ' = 600 N F m s = 360 N
Xét trục quay qua A
M N → B = M P → + M P ' → N B . A B sin α = P . A B 2 . cos α + P ' . A O ' . cos α ⇒ A O ' = 1 , 3 m


Chọn D.
Lấy O’ là vị trí người khi thang bắt đầu trượt.
Theo điều kiện cân bằng lực:
![]()
→NB = Fms = k.NA; NA = P + P’ = 600 N
Fms = 360N
Xét trục quay qua A:


ta có:
nm//ac
bm=cm
=>bn=na
=>nm là đtb của tam giác bac
=>nm = ca/2=0,4
vậy khoảng cánh chân của người đứng trên bật than đối với bức tường là 0,4 m