Cho ngũ giác ABCDE. Có bao nhiêu vectơ được lập ra từ các cạnh và đường chéo của ngũ giác?
A. 5
B. 10
C. 15
D. 20
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
H9
HT.Phong (9A5)
CTVHS
17 tháng 10 2023
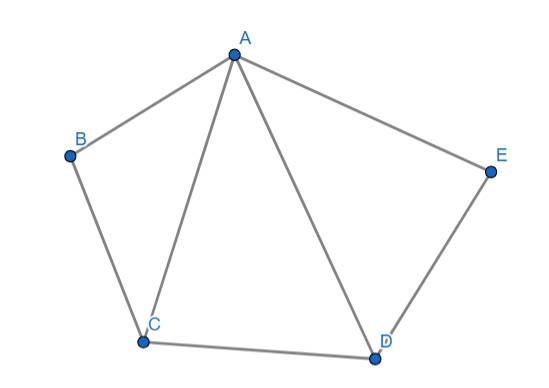
Ta có hình ngũ giác ABCDE ta có 4 cách lập vectơ có điểm cuối là điểm A
Các vectơ lập được là:
\(\overrightarrow{BA};\overrightarrow{CA};\overrightarrow{DA};\overrightarrow{EA}\)
12 tháng 3 2020
cj kham khảo
a) Nối AC; AD
Ngũ giác ABCDE được chia thành 3 tam giác: ΔABC, ΔACD, ΔADE. Tổng các góc trong của mỗi tam giác bằng 1800
Tổng các góc trong của ngũ giác ABCDE là 1800. 3 = 5400
b) Vì ABCDE là ngũ giác đều nên
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=\widehat{E}=\frac{540^0}{5}=108^0\)
Mặt khác ΔABC cân tại B nên
\(\widehat{BAC}+\widehat{BCA}=\frac{180^0-108^0}{2}=36^0\)
\(\Rightarrow\widehat{CAE}=\widehat{ACD}=108^0-36^0=72^0\)
\(\Rightarrow\widehat{EDC}+\widehat{ADC}=108^0+72^2=180^0\)
Suy ra ED // AC hay ED // CF.
Chứng minh tương tự ta có EF // CD
Mặt khác ED = DC (gt)
nên tứ giác CEFD là hình thoi.
PT
1
CM
18 tháng 6 2019
Có 2 tam giác: ABC, ACD, ADE
Có 2 tứ giác: ABCD, ACDE
Có 1 ngũ giác: ABDE
Y
5 tháng 6 2023
\(1,\) Đa giác có 24 đỉnh \(\Rightarrow\) Đa giác có 24 cạnh
Số đường chéo của đa giác là \(C_{24}^2-24=252\) đường chéo.
\(2,\)
\(a,\) Từ các đỉnh của đa giác, lập được \(252+24=276\) đoạn thẳng.
\(b,\) Từ các đỉnh của đa giác, lập được \(A^2_{24}=552\) vectơ khác vectơ-không.
\(c,\) Từ các đỉnh của đa giác, lập được \(C^3_{24}=2024\) tam giác.
* Với điểm đầu là A: Có 4 vectơ được lập ra từ các cạnh và đường chéo của ngũ giác là: A B → ; A C → ; A D → ; A E →
* Tương tự với các đỉnh còn lại.
* Do đó, số vectơ được lập ra từ các cạnh và đường chéo của ngũ giác là 4.5 = 20 vecto
Đáp án D