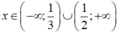Xét dấu của các biểu thức sau :
f(x) = ( -x2+x-1)(6x2-5x+1)
A. f(x) > 0 khi và chỉ khi x ∈ 1 3 ; 1 2
B. f(x) < 0 khi và chỉ khi x ∈ 1 3 ; 1 2
C. f(x)>0 khi và chỉ khi x ∈ - ∞ ; 1 3 ∪ 1 2 ; + ∞
D. f(x)< 0 khi và chỉ khi x ∈ - ∞ ; 1 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)


f(x) = x2 – 5x +4
f(4)= 0; f(2) = -2 < 0; f(-1)= 10 > 0; f(0) = 4 > 0

\(f\left(x\right)=\dfrac{11x+3}{-x^2+5x-7}.\)
Ta có: \(-x^2+5x-7\) là 1 tam thức bậc 2.
\(\left\{{}\begin{matrix}a=-1< 0.\\\Delta=5^2-4.\left(-1\right).\left(-7\right)=-3< 0.\end{matrix}\right.\)
\(\Rightarrow-x^2+5x-7>0\forall x\in R.\)
\(\Rightarrow\) \(f\left(x\right)>0.\Leftrightarrow11x+3>0.\Leftrightarrow x>\dfrac{-3}{11}.\\ f\left(x\right)< 0.\Leftrightarrow11x+3>0.\Leftrightarrow x>\dfrac{-3}{11}.\\ f\left(x\right)=0.\Leftrightarrow x=\dfrac{-3}{11}.\)

Có ![]()
![]()
Đặt t=f(x)+m bất phương trình trở thành: ![]()
![]()
Vậy ![]()
![]()
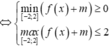
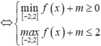
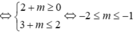
Chọn đáp án B.

Chọn C.
Hàm số đã cho các định trên R \ {2}.
Ta có ![]()
Đặt 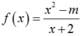 khi x < 3 (m là tham số, m > 0).
khi x < 3 (m là tham số, m > 0).
Ta có 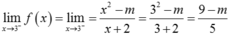 .
.
Để hàm số f(x) có giới hạn khi x → 3 thì 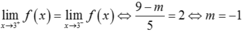 .
.
Chọn A
Ta có –x2+x-1= 0 vô nghiệm,
6x2- 5x+1= 0 khi x= ½ hoặc x= 1/3
Bảng xét dấu
Suy ra f(x) > 0 khi và chỉ khi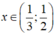
Và f( x)< 0 khi và chỉ khi