Cho khối chóp S. ABC với tam giác ABC vuông cân tại B. AC = 2a, SA vuông góc với mặt phẳng (ABC) và SA = a. Giả sử I là điểm thuộc cạnh SB sao cho S I = 1 3 S B . Thể tích khối tứ diện S AIC bằng
A. a 3 6
B. 2 a 3 3
C. a 3 9
D. a 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có V S . A I C V S . A B C = S I S B = 1 3 ⇒ V S . A I C = 1 3 V S . A B C = 1 3 . 1 3 S A . 1 2 B A . B C
= 1 18 a . B A 2 = 1 18 a . 2 a 2 2 = a 3 9

Chọn B

Ta có B C ⊥ S M . Gọi H là hình chiếu vuông góc của A trên SM. Do
![]() và FE đi qua H.
và FE đi qua H.
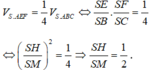
Vậy H là trung điểm cạnh SM. Suy ra tam giác SAM vuông cân tại A
⇒ S A = a 3 2 V S A B C = 1 3 . a 3 2 . a 2 3 4 = a 3 8

\(AB=AC=\dfrac{BC}{\sqrt{2}}=\dfrac{3a}{\sqrt{2}}\)
\(\Rightarrow V_{SABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.2a.\dfrac{1}{2}.\left(\dfrac{3a}{\sqrt{2}}\right)^2=\dfrac{3a^3}{2}\)

Đáp án D
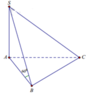
Ta có 2 A B 2 = A C 2 = 2 a 2 2 ⇒ A B = 2 a
Mặt cầu tâm tiếp xúc với mặt phẳng (ABC) có bán kính
S A = A B tan 60 0 = 2 a 3
Diện tích mặt cầu tâm S là: S = 4 π 2 a 3 2 = 48 π a 2