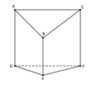
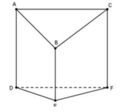
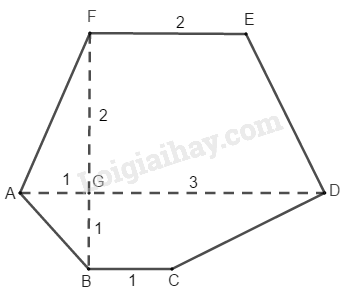
Cho hình đa diện ABCDEF như sau: Biết rằng
∆
A
B
C
là tam giác đều cạnh a, DEF cân tại E; các cạnh AD, BE, CF vuông góc với mặt phẳng (DEF); tứ giác ADFC là hình chữ nhật; AD = CF =
3
a
2
, BE =a. Góc giữa mặt phẳng (ABC) và (DEF) có giá trị gần nhất với: A.
34
o
B.
35
o
C.
36
o
D.
37
...
Đọc tiếp
Cho hình đa diện ABCDEF như sau:
Biết rằng ∆ A B C là tam giác đều cạnh a, DEF cân tại E; các cạnh AD, BE, CF vuông góc với mặt phẳng (DEF); tứ giác ADFC là hình chữ nhật; AD = CF = 3 a 2 , BE =a. Góc giữa mặt phẳng (ABC) và (DEF) có giá trị gần nhất với:
A. 34 o
B. 35 o
C. 36 o
D. 37 o
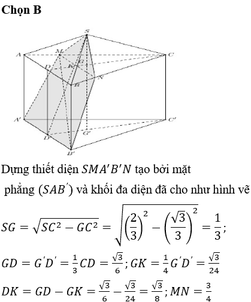
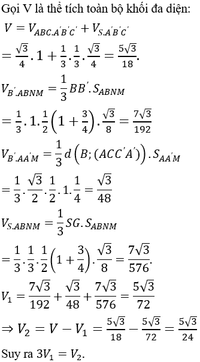
a, Ta có
Đáp án B
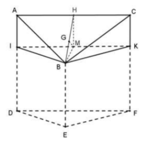
Góc giữa mặt phẳng (ABC) và (DEF) bằng với góc giữa 2 mặt phẳng (ABC) và (BIK) trong đó mặt phẳng (BIK) song song với (DEF)
Vẽ đường cao BH của tam giác đều ABC, suy ra H là trung điểm AC và BH = a 3 2
Gọi M là trung điểm IK. Khi đó HM là đường trung bình của hình chữ nhật AIKC
HM =AI = a 2 và HM song song với AI
Trong mặt phẳng (BHM) vẽ MG ⊥ BH tại G
Do MG ⊥ BH và AC ⊥ MG(AC ⊥ (BHM)) nên MG ⊥ (ABC) (2)
Từ (1) và (2) => góc giữa 2 mặt phẳng (ABC) và (BKI) bằng góc giữa MG với HM, tức góc HMG
Trong ∆ B H M vuông tại M, ta có: