Tính lim x → 0 8 + x 2 3 - 2 x 2
A. 1 12
B. 1 4
C. 1 3
D. 1 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

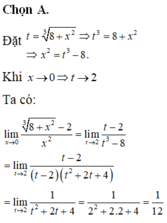

a: \(\lim\limits_{x\rightarrow4}\dfrac{\sqrt{2x+8}-4}{x-4}\)
\(=\lim\limits_{x\rightarrow4}\dfrac{2x+8-16}{\sqrt{2x+8}+4}\cdot\dfrac{1}{x-4}\)
\(=\lim\limits_{x\rightarrow4}\dfrac{2\left(x-4\right)}{\sqrt{2x+8}+4}\cdot\dfrac{1}{x-4}\)
\(=\lim\limits_{x\rightarrow4}\dfrac{2}{\sqrt{2x+8}+4}=\dfrac{2}{\sqrt{2\cdot4+8}+4}\)
\(=\dfrac{2}{\sqrt{8+8}+4}=\dfrac{2}{4+4}=\dfrac{2}{8}=\dfrac{1}{4}\)
b: \(\lim\limits_{x\rightarrow2}\dfrac{x^2-4}{\sqrt{4x+1}-3}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)}{\dfrac{4x+1-9}{\sqrt{4x+1}+3}}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)}{4\left(x-2\right)}\cdot\left(\sqrt{4x+1}+3\right)\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x+2\right)\left(\sqrt{4x+1}+3\right)}{4}\)
\(=\dfrac{\left(2+2\right)\left(\sqrt{4\cdot2+1}+3\right)}{4}=\sqrt{9}+3=6\)
c: \(\lim\limits_{x\rightarrow2}\dfrac{x-2}{2-\sqrt{x+2}}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{x-2}{\dfrac{4-x-2}{2+\sqrt{x+2}}}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{x-2}{2-x}\cdot\left(\sqrt{x+2}+2\right)\)
\(=\lim\limits_{x\rightarrow2}\left(-\sqrt{x+2}-2\right)\)
\(=-\sqrt{2+2}-2=-2-2=-4\)

\(=\lim\limits_{x\rightarrow0}\dfrac{2\left(\sqrt[]{2x+1}-1\right)+2-\sqrt[3]{x^2+x+8}}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{2.2x}{\sqrt[]{2x+1}+1}-\dfrac{x\left(x+1\right)}{\sqrt[3]{\left(x^2+x+8\right)^2}+2\sqrt[3]{x^2+x+8}+4}}{x}\)
\(=\lim\limits_{x\rightarrow0}\left(\dfrac{4}{\sqrt[]{2x+1}+1}-\dfrac{x+1}{\sqrt[3]{\left(x^2+x+8\right)^2}+2\sqrt[3]{x^2+x+8}+4}\right)\)
\(=\dfrac{23}{12}\)

Do quá làm biếng dùng Hoocne tách nhân tử nên chúng ta sẽ sử dụng L'Hopital:
\(\lim\limits_{x\rightarrow1}\frac{4x^6-5x^5+x}{x^2-2x+1}=\lim\limits_{x\rightarrow1}\frac{24x^5-25x^4+1}{2x-2}=\lim\limits_{x\rightarrow1}\frac{120x^4-100x^3}{2}=\frac{120-100}{2}=10\)
\(\lim\limits_{x\rightarrow-3}\frac{x^4-6x^2-27}{x^3+3x^2+x+3}=\lim\limits_{x\rightarrow-3}\frac{4x^3-12x}{3x^2+6x+1}=\frac{-36}{5}\)
\(\lim\limits_{x\rightarrow-2}\frac{2x^3+x^2+12}{-x^2-6x-8}=\lim\limits_{x\rightarrow-2}\frac{6x^2+2x}{-2x-6}=-10\)
\(\lim\limits_{x\rightarrow-2}\frac{-2x^3+x-14}{-2x^3-x^2-12}=\lim\limits_{x\rightarrow-2}\frac{-6x^2+1}{-6x^2-2x}=\frac{23}{20}\)
Con cuối ko phải tích phân dạng vô định \(\frac{0}{0}\) bạn cứ thế thẳng -2 vào là được

a/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2-x+1-x^2-x-1}{\sqrt{x^2-x+1}+\sqrt{x^2+x+1}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-\dfrac{2x}{x}}{\sqrt{\dfrac{x^2}{x^2}-\dfrac{x}{x^2}+\dfrac{1}{x^2}}+\sqrt{\dfrac{x^2}{x^2}+\dfrac{x}{x^2}+\dfrac{1}{x^2}}}=-\dfrac{2}{1+1}=-1\)
b/ \(=\lim\limits_{x\rightarrow2}\dfrac{4x+1-9}{\left(x-2\right)\left(x+2\right)\left(\sqrt{4x+1}+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{4\left(x-2\right)}{\left(x-2\right)\left(x+2\right)\left(\sqrt{4x+1}+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{4}{\left(x+2\right)\left(\sqrt{4x+1}+3\right)}=\dfrac{4}{\left(2+2\right)\left(\sqrt{4.2+1}+3\right)}=\dfrac{1}{6}\)
c/ \(=\lim\limits_{x\rightarrow-2}\dfrac{2x+5-1}{\left(x-2\right)\left(x+2\right)\left(\sqrt{2x+5}+1\right)}=\lim\limits_{x\rightarrow-2}\dfrac{2}{\left(x-2\right)\left(\sqrt{2x+5}+1\right)}=\dfrac{2}{\left(-2-2\right)\left(\sqrt[2]{2.\left(-2\right)+5}+1\right)}=\dfrac{2}{\left(-4\right).2}=-\dfrac{1}{4}\)

a. \(lim_{x\rightarrow3}\dfrac{x^3-27}{3x^2-5x-2}=\dfrac{3^3-27}{3.3^2-5.3-2}=\dfrac{0}{10}=0\)
b. \(lim_{x\rightarrow2}\dfrac{\sqrt{x+2}-2}{4x^2-3x-2}=\dfrac{\sqrt{2+2}-2}{4.2^2-3.2-2}=\dfrac{0}{8}=0\)
c. \(lim_{x\rightarrow1}\dfrac{1-x^2}{x^2-5x+4}=lim_{x\rightarrow1}\dfrac{\left(1-x\right)\left(x+1\right)}{\left(x-1\right)\left(x-4\right)}=lim_{x\rightarrow1}\dfrac{-\left(x+1\right)}{x-4}=\dfrac{-\left(1+1\right)}{1-4}=\dfrac{2}{3}\)
d. Câu này mình chịu, nhìn đề hơi lạ so với bình thường hehe

Lời giải:
a)
\(\lim\limits_{x\to +\infty}\frac{\sqrt[3]{x^3+2x^2-4x+1}}{\sqrt{2x^2+x-8}}=\lim\limits_{x\to +\infty}\frac{\sqrt[3]{1+\frac{2}{x}-\frac{4}{x^2}+\frac{1}{x^3}}}{\sqrt{2+\frac{1}{x}-\frac{8}{x^2}}}\)
\(=\frac{1}{\sqrt{2}}\)
b)
\(\lim\limits_{x\to -\infty}\frac{\sqrt{x^2-2x+4}-x}{3x-1}=\lim\limits_{x\to -\infty}\frac{\sqrt{1-\frac{2}{x}+\frac{4}{x^2}}+1}{-3+\frac{1}{x}}=\frac{-1}{3}\)