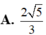
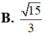
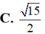
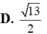
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
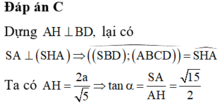
Đáp án D
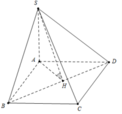
Kẻ A H ⊥ B D với H ∈ B D ta có S H ⊥ B D , từ đó suy ra S H A ^ là góc giữa hai mặt phẳng (SBD) và (BACD).
Ta có 1 A H 2 = 1 A B 2 + 1 A D 2 = 1 a 2 + 1 4 a 2 = 5 4 a 2 ⇒ A H = 2 a 5
Vậy tan S H A ^ = S A A H = a 3 2 a 5 = 15 2
Đáp án C
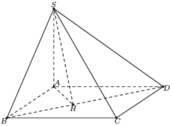
Dựng A H ⊥ B D , lại có
S A ⊥ S H A ⇒ S B D ; A B C D ^ = S H A ^
Ta có A H = 2 a 5 ⇒ tan α = S A A H = 15 2
Đáp án C
Kẻ AH ⊥BD
Khi đó 
Mà 
nên góc giữa (SBD) và (ABCD) là SHA=α.
Suy ra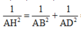 
Do đó 
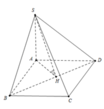
(SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=3/2
=>góc SDA=56 độ
