Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60 o . Gọi M và N lần lượt là trung điểm của AB và CD.
Góc giữa hai mặt phẳng (ACD) và (BCD) là:
A. A C B ⏜
B. A N B ⏜
C. A D B ⏜
D. M N B ⏜
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có CD ⊥ (ABN) (do BN ⊥ CD và AN ⊥ CD) ⇒ (BCD) ⊥ (ABN)
Đáp án C

Phương án A sai vì nếu CD ⊥ (ABD) thì CD ⊥ AD. Nhưng tam giác ACD cân tại A nên CD không thể vuông góc với AD
Phương án B sai vì tương tự như trên thì CD không thể vuông góc với AC
Phương án C đúng vì CD ⊥ AN (AN là đường trung tuyến của tam giác cân CAD tại A) và CD ⊥ MN ⇒ CD ⊥ (ABN)
Phương án D sai vì CD không vuông góc với MD do chứng minh trên.
Đáp án C

Ta có: A B → . C D → = A B → A D → − A C → = A B → . A D → − A B → . A C →
= A B → . A D → . cos B A D − A B → . A C → cos B A C
= A B 2 . cos 60 ° − A B 2 cos 60 ° (do AB = AC = AD và B A C ^ = B A D ^ = 60 ° )
= 0
Suy ra A B ⊥ C D hay góc giữa hai vecto A B → và C D → là 90 ° .
ĐÁP ÁN C

Loại phương án A và B vì BC và CD không phải là hình chiếu của CM trên (BCD)
Phương án C đúng vì :

Đáp án C

Đáp án C
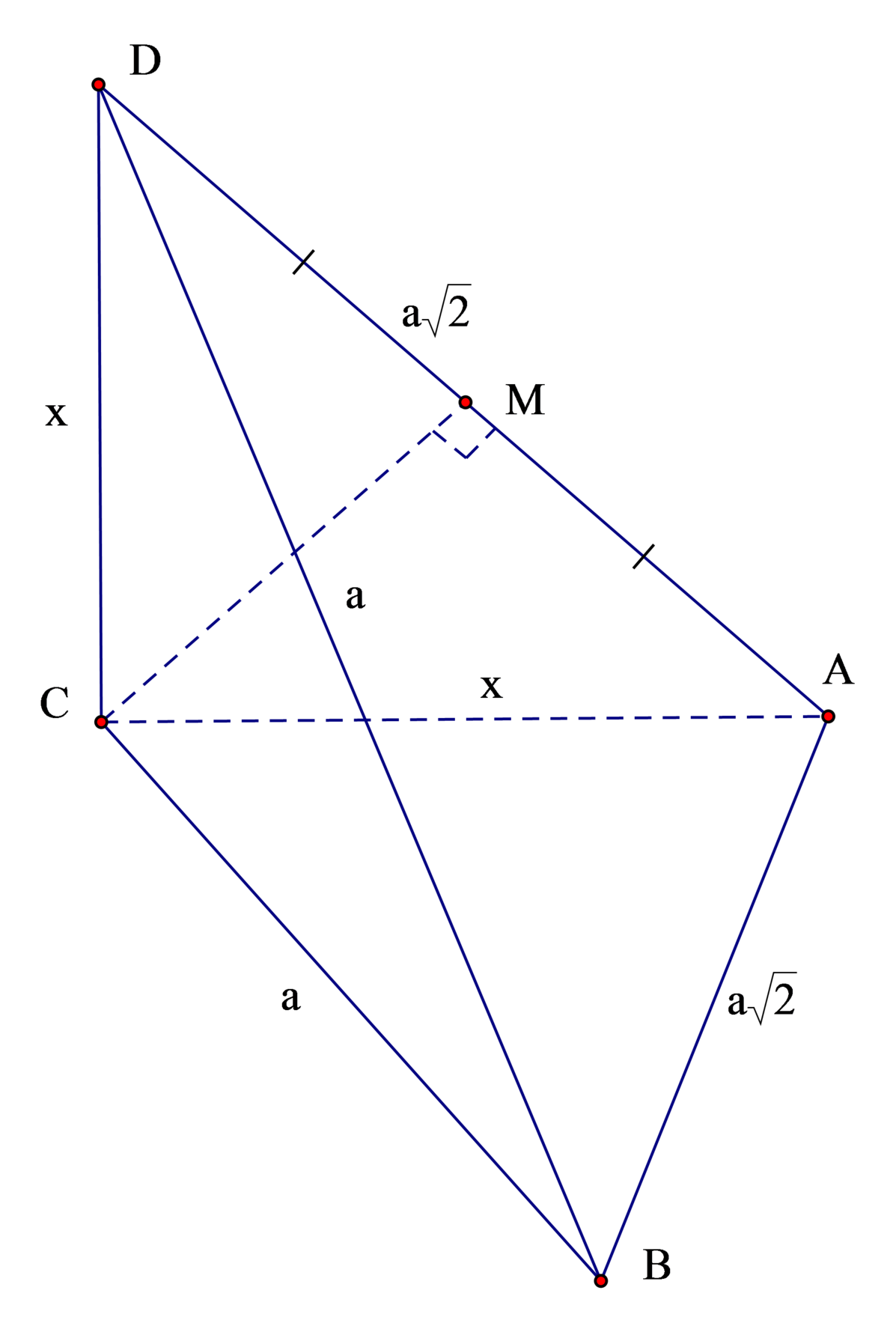
Gọi h là khoảng cách từ B → A C D
⇒ h = a 3 2 ⇒ S Δ A C D = 3 V A B C D h = 3 a 3 3 12 a 3 2 = a 2 2
Gọi M là trung điểm AD ⇒ C M ⊥ A D .
⇒ C M = 2 S A C D A D = 2. a 2 2 a 2 = a 2 2 = 1 2 A D
⇒ Δ A C D vuông tại C ⇒ C A = C D = a
Δ C A D = Δ C B A C . C . C ⇒ A C D ^ = A C B ^ = 90 0
⇒ A C ⊥ C D A C ⊥ C B ⇒ A C ⊥ B C D ⇒ A C D ⊥ B C D
Hay góc giữa hai mặt phẳng bằng 90 0

Chọn C
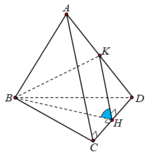
Gọi H là trung điểm cạnh CD và K là trung điểm cạnh AD.
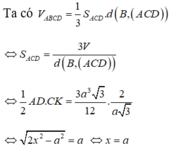
Tam giác ACD có CA=CD=x=a ; AD = a 2 => tam giác ACD vuông cân tại C
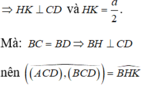
Mặt khác:
Tam giác ABD có:
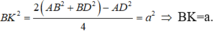
Tam giác BHK có:
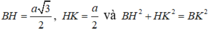
=> Tam giác BHK vuông tại H ⇒ B H K ^ = 90 o hay A C D , B C D ^ = 90 o
Các tam giác ABC và ABD là tam giác đều ⇒ tam giác ACD cân
⇒ BN ⊥ CD và AN ⊥ CD ⇒ góc ANB là góc của hai mặt phẳng (ACD) và (BCD)
Đáp án B