Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA = AB = 2AD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Bán kính của mặt cầu ngoại tâm B cắt SC theo một dây có độ dài 2a/3 là:
A. 2 a 3 3
B. 2 a 2 3
C. a
D. a 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Do (SAB) ⊥ (ABCD) và (SAD) ⊥ (ABCD) ta có SA ⊥ (ABCD). Theo định lí ba đường vuông góc ta có BC ⊥ SB.
Hạ BH ⊥ SC tại H. Xét tam giác vuông SBC ta có:
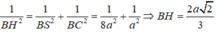
Ta có mặt cầu S(B;r) cắt đường thẳng SC theo một dây cung có độ dài 2a khi và chỉ khi ta có
![]()

Đáp án C
Ta có mặt cầu S(A;r) cắt mặt phẳng (SBD) theo một đường tròn có bán kính bằng a khi và chỉ khi ![]()
Hạ AK ⊥ BD tại K, hạ AH ⊥ SK tại H. Do BD ⊥ AK và BD ⊥ SA nên BD ⊥ (SAK), suy ra BD ⊥ AH. Mặt khác AH ⊥ SK nên ta có AH ⊥ (SBDB) hay d(A; (SBD)) = AH. Xét tam giác vuông SAK và tam giác vuông ABD ta có:
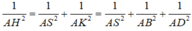
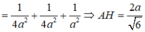
Khi đó ta có:
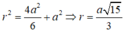

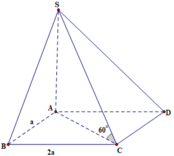
+Vì S A B ⊥ A B C D , S A D ⊥ A B C D mà S A B ∩ S A D = S A nên S A là đường cao của khối chóp
+ Xét tam giác vuông S A C
S A = tan 60 o . A C = 3 . a . 5 = a 15

Đáp án D
Theo định lí ba đường vuông góc ta có hai tam giác SBC và SDC lần lượt vuông góc tại B, D. Gọi I là trung điểm của SC thì ta có: IA = IB = ID = SC/2 = IS = IC nên I là tâm mặt cầu ngoại tiếp hình chóp. Bán kính mặt cầu ngoại tiếp hình chóp là 

Đáp án A
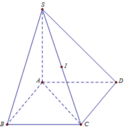
Gọi I là trung điểm của SC. Khi đó I là tâm mặt cầu ngoại
tiếp hình chóp S.ABCD
Ta có: S C = S A 2 + A C 2 = 2 a 2 + 2 a 2 = a 6
Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD là:
R = S C 2 = a 6 2
Đáp án C
Từ giả thiết ta có SA ⊥ (ABCD), theo định lí ba đường vuông góc ta có tam giác SBC vuông tại B. Gọi S(B,r) là mặt cầu tâm B cắt SC theo một dây có độ dài 2a/3. Khi đó ta tính được: